1. 定义

在概率论与统计学的背景下，概率分布函数是一种数学函数，它能够给出可能发生的结果的发生概率。更确切地说，它是对随机事件发生概率的数学描述。 概率分布可以分成两种类型：

  1. 离散型
  2. 连续型

本文简单总结概率函数中的几个常见的概念。

2. 概率分布

2.1 离散型

函数输入为一个可能发生的事件，返回该事件发生的概率。这个函数称为概率分布函数：Probability Mass Function (PMF)：

\[p(x_i) = P(X=x_i)\]

其中\(x_i\)表示某个可能发生的具体事件。由于离散型随机变量是可穷举的，所以获得事件发生的概率比较方便。

2.2 连续型

扩展到连续型变量后，不能像离散型一样方便了，因为任何一个可能的值发生的概率都为0。可以这么理解：在一个二维平面中随机打一个点，打中原点是可能发生的事情，但是概率为0。所以，为了衡量连续型变量的概率，提出概率密度函数：Probability Density Function (PDF)。

如何理解“密度”这个词语？我个人的理解是这样的：往一个平面随机洒一把黄豆（不考虑出发点、高度或黄豆互相撞击等的影响），假设平面均匀、平滑，那么黄豆掉落到每个地方的概率是一样的，如下图（左）；但如果平面不均匀、不平滑，黄豆受到外界因素的影响，不均匀的分散在了平面上，如下图（右）。

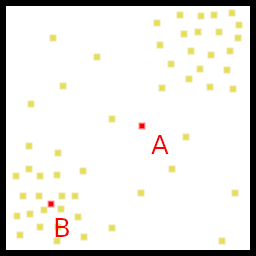
如果现在提问：往右图的平面再丢一个黄豆，请问它更可能接近\(A\)点还是\(B\)点？答案当然是\(B\)点，虽然我们不知道平面到底是什么样的，但是可以从第一次随机抛撒中得到信息，\(B\)点附近的黄豆更密集，\(A\)点附近黄豆稀疏，所以黄豆更可能掉落到\(B\)附近。

概率密度函数就是反映“密集程度”的函数，它能够向上图一样描述出某个范围的密度。虽然它不能直接等同于概率，但能一定程度反映概率。

假设概率密度函数为\(f(x)\)，点落在\((a, b)\)范围内的概率为：

\[Pr[a \le X \le b]= \int_a^b f(x) dx\]

常见的高斯分布的概率密度函数为： \(f(x) = \frac{1}{\sqrt{2\pi}\sigma}*exp(-\frac{(x-\mu)^2}{2\sigma^2})\)

误区：认为将\(x\)代进去，就获得了取\(X=x\)的概率。

直观地看，\(f(x)dx\)可以看作是\(X\)落在无限小的区间\([x, x+dx]\)的概率。

2.3 累积密度函数

累积概率密度：Cumulative Density Function (CDF)的定义为：

\[F(x) = \int_{-\infty}^x f(u) du\]

并且

\[f(x) = \frac{d}{dx} F(x)\]

3. 其他描述概率的方式

当变量不止一个时，有以下描述概率的方式，假设有两个变量分别为\(X\)和\(Y\)。

3.1 边缘概率

当\(X=a\)时的概率，即\(P(X=a)\) for all \(Y\)。

3.2 条件概率

当\(Y=b\)发生时\(X=a\)发生的概率，即\(P(X=a|Y=b)\)。

3.3 联合概率

\(X=a\)和\(Y=b\)同时发生的概率，即\(P(X=a, Y=b)\)。

当两个事件相互独立时，\(P(X=a, Y=b) = P(X=a) * P(Y=b)\)。

4. Normalizing constant

对于贝叶斯定理：

\[p(\theta|data) = \frac{p(data|\theta) \ p(\theta)}{p(data)}\]

其中：

\(p(\theta \vert data)\)为后验概率（Posterior）

\(p(data \vert \theta)\)为似然（Likelihood）

\(p(\theta)\)为先验（Prior）

\(p(data)\)为证据（evidence），也叫Marginal（它是边缘概率），也叫Normalizing constant，因为它本质上是一个scaler。这个Normalizing constant是为了让PDF对取值范围积分后为1。