1. 提出问题

目前主流的深度生成模型（deep generative model）有：

  • VAE
  • GANs

这两种技术都可以解决密度估计（density estimation）问题，也就是找出数据\(X\)的分布。对于数据\(X=\{x_1, x_2, \cdots, x_n\}\)，假设它是某个随机分布抽取出来的样本。如果我们能得到这个随机分布的话，就可以无限制地生成样本。但这个分布是难以获得的，必须用已有的数据通过训练得到或逼近它。

为了达到上述目的，首先选择一个已知的随机分布（例如高斯分布）\(Z \sim N(\mu, \sigma^2)\)，以上两种技术学习参数去将已知分布\(Z\)映射/转移到数据\(X\)的未知分布中。一旦参数学习完毕，我们就能够通过已知的概率分布中的数据，找到数据分布中对应的数据，以达到生成的目的。

那么VAE和GANs有什么不足的地方？它们学习到的是分布的隐式表达，无法获得数据\(X\)分布的确切表达。换句话说，你给我任意从高斯分布采样的数据\(z\)，我不仅能找到它在数据\(X\)分布中的映射，还能计算出密度\(p(z)\)；但是给我任意一个数据\(x\)，VAE和GANs不能给出密度\(q(x)\)。

Normalizing flows（NF）也叫标准化流，就是为解决这个问题而诞生的。

我们要做的事情框架为：

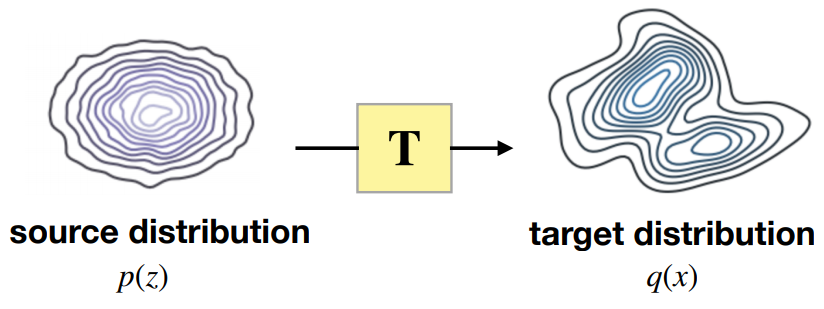
输入已知概率分布（source distribution），经过Transformation，得到目标概率分布（target distribution）。

2. 初步理解

2.1 单变量的映射

对于单变量的映射：\(T:Z\rightarrow X\)

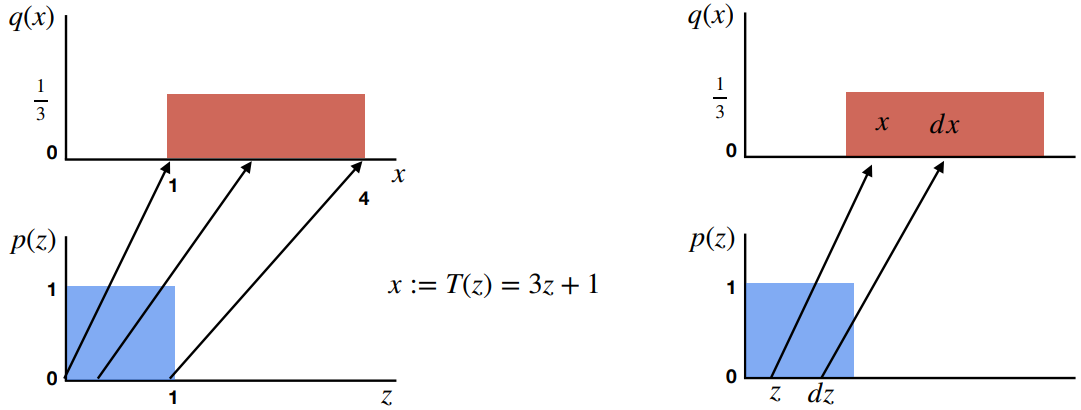
如上图，考虑一个变量\(z\)服从均匀分布\(Uniform(0,1)\)，经过一个简单的线性映射\(T\)（\(x=3z+1\)）后到了新的分布中。由于累积密度的性质，映射前和映射后的分布所占的面积是相等的，所以有： \(\begin{aligned} p(z)dz &= q(x)dx \\ q(x) &= p(z)|\frac{dz}{dx}| \\ q(x) &= p(z)|\frac{\partial{T(z)}}{\partial{z}}|^{-1} \end{aligned} \tag{1}\)

2.2 多变量的映射

对于多变量的映射：\(T:\mathbb{R}^d\rightarrow \mathbb{R}^d\)

已知\(\vec x \subseteq \mathbb{R}^d\)，\(\vec z \subseteq \mathbb{R}^d\)，\(\vec x = (x_1, x_2, \cdots, x_d)\)，\(\vec z = (z_1, z_2, \cdots, z_d)\)。

\(T: \vec z \rightarrow \vec x\)，\(T = (T_1, T_2, \cdots, T_d)\)

于是有：

\[x_1 = T_1(\vec z) = T_1(z_1, z_2, \cdots, z_d) \\ x_2 = T_2(\vec z) = T_2(z_1, z_2, \cdots, z_d) \\ \cdots \\ x_d = T_d(\vec z) = T_d(z_1, z_2, \cdots, z_d)\]

所以： \(q(\vec x) = p(\vec z)|det(\nabla_{\vec z}T(\vec z))|^{-1} \tag{2}\)

其中：

\[\nabla_{\vec z}T(\vec z)) = \left[ \begin{matrix} \frac{\partial{T_1}}{\partial{z_1}} & \frac{\partial{T_1}}{\partial{z_2}} & \cdots &\frac{\partial{T_1}}{\partial{z_d}} \\ \frac{\partial{T_2}}{\partial{z_1}} & \frac{\partial{T_2}}{\partial{z_2}} & \cdots &\frac{\partial{T_2}}{\partial{z_d}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial{T_d}}{\partial{z_1}} & \frac{\partial{T_d}}{\partial{z_2}} & \cdots &\frac{\partial{T_d}}{\partial{z_d}} \\ \end{matrix} \right]\]

这也被称为雅可比矩阵（Jacobian matrix）。式\((2)\)是NF的核心。

3. 学习流程

给定一个数据集\(D = \{x_1, x_2, x_3, \cdots, x_n\} \sim q(x)\)，我们要学习出密度函数\(q(x)\)，本质上就是学习转换函数\(T\)的参数，既然“模型已定，参数未知”，则使用最大似然估计：

理论上来说是按照上面的学习流程：最大似然估计，但是现在又遇到问题了！

  • \(z_i\)怎么获得？\(z_i = T^{-1}(x_i)\)，要通过\(T^{-1}\)才能获得；
  • 雅可比行列式的计算量太大。

解决方案：

  1. 对于第一个问题，必须要求换转函数\(T\)是可逆的；

  2. 对于第二个问题，令\(T\)变为“三角形状”的映射（increasing triangular maps）：

\[\begin{aligned} x_1 &= T_1(z_1) \\ x_2 &= T_2(z_1, z_2) \\ x_3 &= T_3(z_1, z_2, z_3) \\ &\vdots \\ x_d &= T_d(z_1, z_2, z_3, \cdots, z_d) \end{aligned}\]

经过这种设定，雅可比矩阵就变为：

\[\nabla_{\vec z}T(\vec z)) = \left[ \begin{matrix} \frac{\partial{T_1}}{\partial{z_1}} & 0 & \cdots & 0 \\ \frac{\partial{T_2}}{\partial{z_1}} & \frac{\partial{T_2}}{\partial{z_2}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial{T_d}}{\partial{z_1}} & \frac{\partial{T_d}}{\partial{z_2}} & \cdots &\frac{\partial{T_d}}{\partial{z_d}} \\ \end{matrix} \right]\]

在计算行列式时只需要将对角线的值相乘即可，大大减少计算量。

4. 标准化流

NF的研究就是“研究如何建立满足上述条件的转换函数\(T\)，并训练他们获得目标数据的分布”。

整体的学习框架如下图：

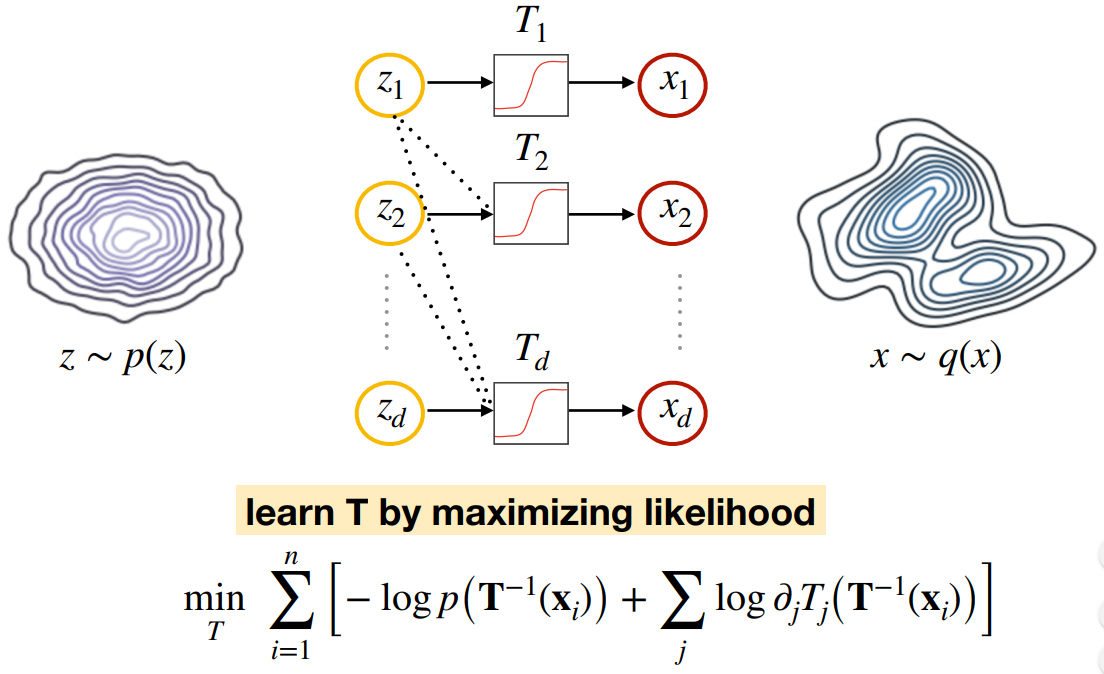
如果能够获得这样的转换函数\(T\)，那么就能够通过式\((2)\)计算出\(q(x)\)，问题得到解决。

那么为什么称为“Flows”呢？因为转换函数\(T\)可以叠加很多层，多层叠加可形成“流式”结构。

\[q(x) = q(z)|det \frac{\partial f^{-1}}{\partial x}| = q(z)|det \frac{\partial f}{\partial z}|^{-1} \tag{3}\] \[z_K = f_K \circ f_{K-1} \circ \cdots \circ f_2 \circ f_1(z_0)\] \[lnq_K(z_K) = ln q_0(z_0) - \sum_{k=1}^K ln|det \frac{\partial f_k}{\partial z_{k-1}}|\]

式\((3)\)也叫做Change of variable formula。

下面是用PyTorch实现的标准化流的简单教程：

Tutorial of normalizing flows with PyTorch: normalizing-flows-tutorial-pytorch

参考

Normalizing Flows Tutorial

cs480-lecture23 （Source of the images on this page）