接着上一篇文章的思路（Ensemble Learning I (Bagging and Boosting)），下面介绍Boosting方法的另外两种拓展。（Formula部分提供理解本文推导所需的数学公式）

1. GBDT

1.1 Gradient Boosting

Idea:

  • 延续Boosting的思路，假设在第\(t\)阶段训练得到的学习器为\(f_t = \sum_{i=0}^t \alpha_i h_i\)；
  • 训练学习器\(h_{t+1}\)去估计negative gradient：
\[h_{t+1} \approx - \frac{\partial L(y, f_t(x))}{\partial f_t(x)}\]
  • 得到新的基学习器\(h_{t+1}\)后，优化权重\(\alpha_{t+1}\)：
\[\alpha_{t+1} = \arg \min_{a} L(Y, f_t(X) + \alpha_{t+1} h_{t+1}(X))\]
  • 得到新学习器\(f_{t+1}\)：
\[f_{t+1} = f_t + \alpha_{t+1} h_{t+1}(x)\]

整个过程在模拟梯度下降，随着基学习器数量的增加，集成模型越接近真实模型。

当损失函数\(L\)在其中是什么角色呢？当损失函数为\(MSE\)时：

\[\begin{aligned} - \frac{\partial L(y, f_t(x))}{\partial f_t(x)} &= - \frac{\partial \frac{1}{2} (y - f_t(x))^2}{\partial f_t(x)} \\ &= y - f_t(x) \end{aligned} \tag{1}\]

其中\(y - f_t(x)\)为残差。因此对于做回归任务的GBDT来说，当损失函数使用\(MSE\)时就相当于让基学习器不断拟合残差。

2. XGBoost

XGBoost的全称是：eXtreme Gradient Boosting。本质上也是一种梯度加速算法。

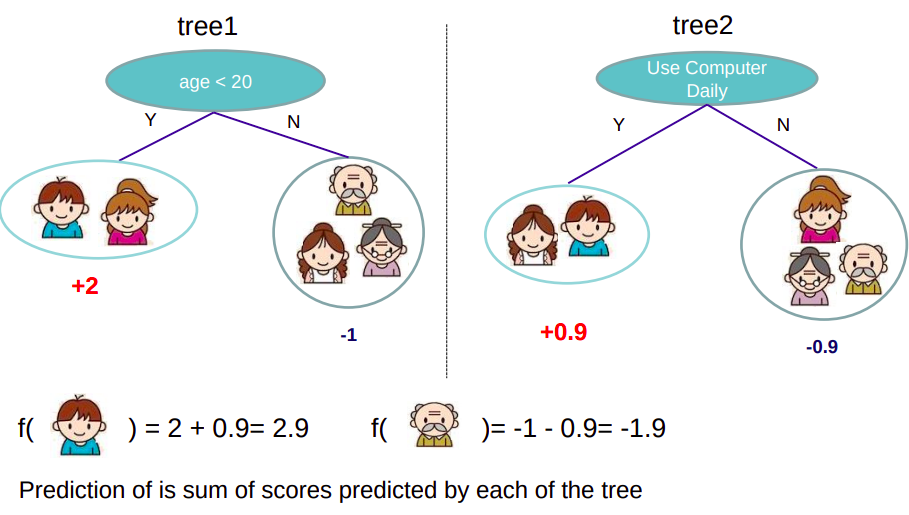
树集成的最终目的是达到上图的效果，学习多个回归树（叶子节点输出分数，代表在某输入下某类别的得分），通过得分相加集成。

重新整理一下GBDT任务的学习流程，第\(t\)轮训练我们的目标函数为：

\[\begin{aligned} Obj^{(t)} &= \sum_{i=1}^N L(y_i, \hat y_i^{(t)}) + \sum_{j=1}^t \Omega(f_j) \\ &= \sum_{i=1}^N L(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \end{aligned} \tag{2}\]

其中\(\Omega\)为正则项。假设采用平方损失，则上式写成：

\[\begin{aligned} Obj^{(t)} &= \sum_{i=1}^N (y_i - (\hat y_i^{(t-1)} + f_t(x_i)))^2 + \Omega(f_t) \\ &= \sum_{i=1}^N (\underbrace{y_i - \hat y_i^{(t-1)}}_{residual} - f_t(x_i))^2 + \Omega(f_t) \end{aligned} \tag{3}\]

2.1 损失函数

现在采用泰特展开来定义一个近似的目标函数：

\[\begin{aligned} Obj^{(t)} &= \sum_{i=1}^N L(y_i, \hat y_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) \\ &= \sum_{i=1}^N (L(y_i, \hat y_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)) + \Omega(f_t) \\ \end{aligned} \tag{4}\]

其中，\(g_i = \frac{\partial L(y_i, \hat y_i^{(t-1)})}{\partial \hat y_i ^{(t-1)}}\)，\(h_i = \frac{\partial^2 L(y_i, \hat y_i^{(t-1)})}{\partial^2 \hat y_i ^{(t-1)}}\)。联系泰勒二阶展开的公式，\(x\)对应目标函数的\(\hat y_i^{(t-1)}\)，\(\Delta x\)对应目标函数的\(f_t(x_i)\)。

去掉式\((4)\)中的常数项得到：

\[\begin{aligned} Obj^{(t)} &= \sum_{i=1}^N (g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)) + \Omega(f_t) \end{aligned} \tag{5}\]

所以目标函数只依赖每个数据点在误差函数上的一阶导数和二阶导数。

2.2 正则项

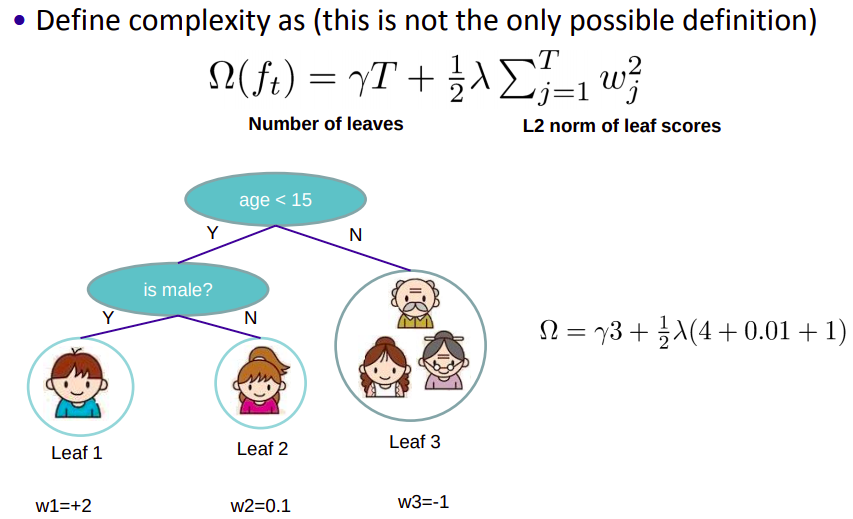
由于XGBoost使用的基学习器是CART树，所以模型复杂度由叶子节点个数\(T\)和叶子节点输出分数\(w\)（L2正则化）决定：

\[\Omega(f_t) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \tag{6}\]

式\((6)\)相当于对树模型添加L1和L2正则化。

2.3 完整目标函数

定义\(q\)函数将输入\(x\)映射到某个叶子节点上，则\(f_t(x) = w_{q(x)}\)，定义每个叶子节点\(j\)上的样本集合为\(I_j = \{i \vert q(x_i) = j\}\)。将式\((5)\)和\((6)\)结合在一起得到：

\[\begin{aligned} Obj^{(t)} &= \sum_{i=1}^N (g_i f_t(x_i) + \frac{1}{2}h_i f_t^2(x_i)) + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{i=1}^N (g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2) + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{j=1}^T (\sum_{i \in I_j} g_i w_j + \frac{1}{2} \sum_{i \in I_j} h_i w_j^2) + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{j=1}^T (G_j w_j + \frac{1}{2} (H_j + \lambda) w_j^2) + \gamma T \end{aligned} \tag{7}\]

其中，\(G_j = \sum_{i \in I_j} g_i\)，\(H_j = \sum_{i \in I_j} h_i\)

2.4 确定树结构

获得了最终目标函数后，此时的任务是搜索合适的“树结构”使得目标函数最小。假设已经知道了树结构，对\(w\)求导并使导数为0，可以得到每个叶子节点分数：

\[w_j = - \frac{G_j}{H_j + \lambda} \tag{8}\]

将式\((8)\)代入式\((7)\)得到：

\[\begin{aligned} Obj^{(t)} &= \sum_{j=1}^T (G_j w_j + \frac{1}{2} (H_j + \lambda) w_j^2) + \gamma T \\ &= \sum_{j=1}^T (- \frac{G_j^2}{H_j + \lambda} + \frac{1}{2} \frac{G_j^2}{H_j + \lambda}) + \gamma T \\ &= -\frac{1}{2} \sum_{j=1}^T (\frac{G_j^2}{H_j + \lambda}) + \gamma T \end{aligned} \tag{9}\]

如下图所示，得到的目标函数结果越小越好。

在进行节点分裂时，ID3采用信息增益，C4.5采用信息增益率，CART采用Gini系数，XGboost采用什么呢？

观察式\((9)\)，为了使得目标函数尽可能小，要求\(\frac{G_j^2}{H_j + \lambda}\)尽可能大，所以采用以下准则计算增益：

\[Gain = \frac{1}{2} [\underbrace{\frac{G_L^2}{H_L + \lambda}}_{分割后左子树分数} + \underbrace{\frac{G_R^2}{H_R + \lambda}}_{分割后右子树分数} - \underbrace{\frac{(G_L + G_R)^2}{H_L + H_R + \lambda}}_{分割前的节点分数}] - \underbrace{\gamma}_{增加一个节点的复杂度代价}\]

Gain值越大，说明分裂后使得目标函数下降越多，越好。

以上是XGBoost的原理部分，在工业应用上还有很多优化的地方，例如并行优化、内存优化、存储+IO优化等等，详情可以移步到参考中。

3. XGBoost与GBDT的联系与区别

联系：

  1. XGBoost实际上是GBDT的一种高级系统实现，其本质上也是GB；

区别：

  1. GBDT只用到了一阶导数信息，XGBoost采用二阶泰勒展开，用到了二阶导数信息；
  2. XGBoost的目标函数自带正则项，相当于预剪枝。正则项相当于降低模型variance，防止过拟合；
  3. XGBoost支持很好的并行，这种并行是特征级上的并行，不是树级的并行；
  4. XGBoost的基学习器除了树，也可以用线性分类器；
  5. 借鉴了RF的做法，XGBoost自带行抽样（样本抽样）也列抽样（特征抽样），防止过拟合；
  6. XGBoost能够自适应学习对缺失值的处理；
  7. XGBoost带有Shrinkage衰减策略，每次添加新的模型，会减少该模型的权重，相当于“逐步降低学习率”的过程。

Formula

泰勒二阶展开（相当于对\(f(x + \Delta x)\)在x=x处做泰勒展开，可阅读文章Taylor Expansion帮助理解）：

\[f(x + \Delta x) \approx f(x) + f'(x) \Delta x + \frac{1}{2} f''(x) \Delta x^2\]

参考

Chen, Tianqi, and Carlos Guestrin. “Xgboost: A scalable tree boosting system.” Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. ACM, 2016.
BoostedTree
Introduction to Boosted Trees
集成学习（三）XGBoost