HOW and WHY Logistic Regression Works
1. Logistic regression
Logitstic Regression (LR) 是解决二分类问题(0或1)的线性模型,它的输出具有概率意义。相比于普通的线性模型,LR只多了一个非线性函数Sigmoid,去掉它LR就会变成线性回归。
1.1 Sigmoid function
Sigmoid函数相信大家都不陌生,不需赘述,在这里写出公式:
\[y = \frac{1}{1+e^{-z}} \tag{1}\]它是一个定义域为\((-\infty, +\infty)\),值域为\((0, 1)\)的函数。在LR算法中,\(z\)即表示回归方程。
1.2 Decision boundary
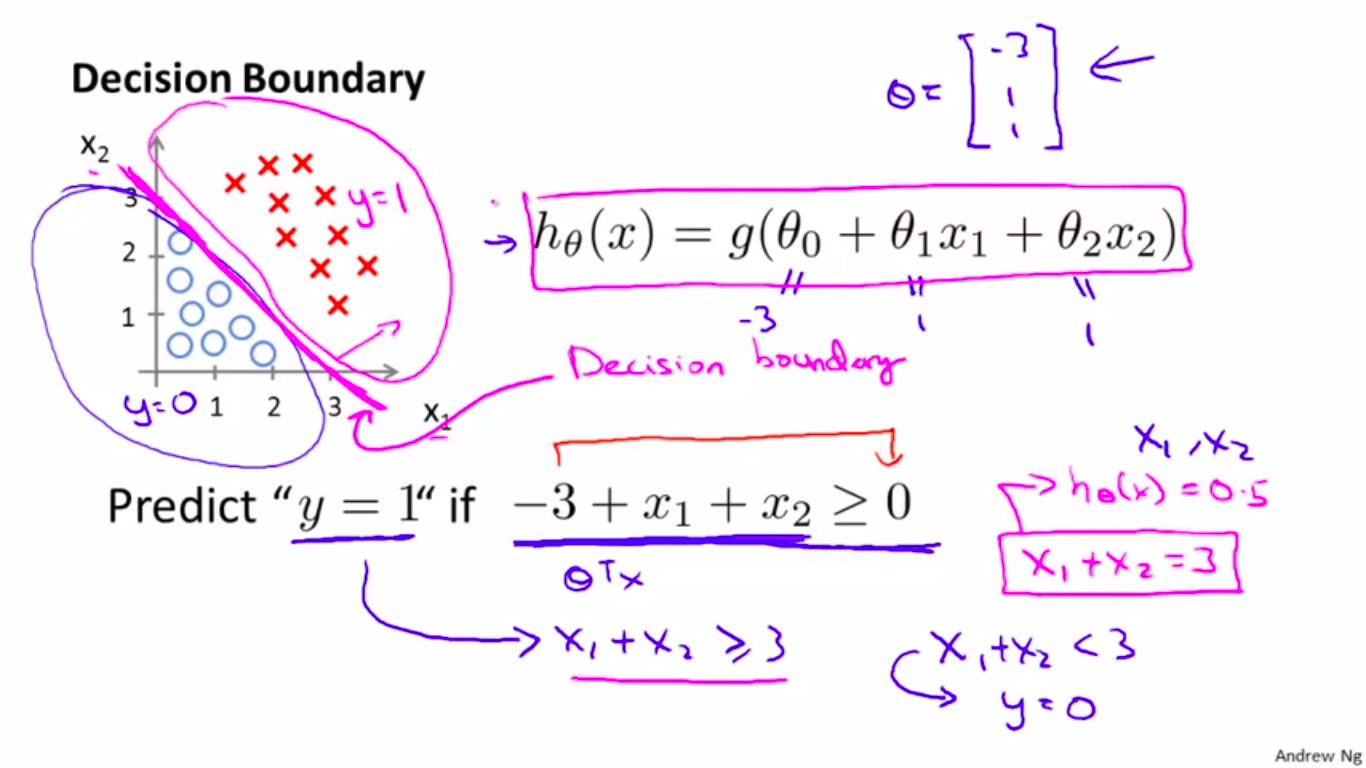
决策边界是由回归函数决定的。
如上图所示,回归函数被定义为:\(z = \theta_0 + \theta_1 x_1 + \theta_2 x_2\),这样一阶的形式能够决定平面中的一条线。
如果数据分布复杂,没有办法用一条线将数据分开呢?增加回归方程的复杂度即可。

如上图所示,增加回归函数复杂度后拟合出来的决策边界是一个圆形,正好将正负类分开。如果希望决策边界更加复杂,只需持续增加多项式的阶数。
2. 数学原理
假设回归模型为:
\[z = wx + b \tag{2}\]经过Sigmoid函数后:
\[p(x) = y = \frac{1}{1+e^{-z}} \tag{3}\]其中,\(p(x)\)表示样本\(x\)为正类的概率。自然,样本\(x\)为负类的概率为:
\[1-p(x) = \frac{e^{-z}}{1+e^{-z}} \tag{4}\]到目前为止我们定义了模型,现在要求解模型参数,又到了熟悉的“模型已定,参数未知”的环节,采用极大似然估计(用\(\theta\)表示模型所有参数):
\[\begin{aligned} L(\theta) &= \prod_{i=1}^N p(x_i)^{y_i} \times (1-p(x_i))^{1-y_i} \\ \ln L(\theta) &= \sum_{i=1}^N y_i \ln p(x_i) + (1-y_i) \ln (1-p(x_i)) \\ &= \sum_{i=1}^N \ln \frac{p(x_i)}{1-p(x_i)} + \ln (1-p(x_i)) \\ &= \sum_{i=1}^N y_i z - \ln (1+e^z) \end{aligned} \tag{5}\]接下来计算偏导求梯度,由于我们需要最大化\(\ln L\),相当于最小化\(- \ln L\):
\[\begin{aligned} \frac{\partial (- \ln L)}{\partial w} &= \frac{1}{1+e^{w x_i + b}} e^{w x_i + b} x_i - x_i y_i \\ &= \frac{1}{1+e^{-z}} x_i - x_i y_i\\ &= p(x_i)x_i - x_i y_i\\ &= (p(x_i) - y_i) x_i \end{aligned} \tag{6}\]最后进行参数更新。以上就是LR如何工作以及LR为什么能工作的解释。