1. 最小二乘法

最小二乘法（Least squares method）是一种数学优化方法，通过最小化误差的平方和寻找最优解。

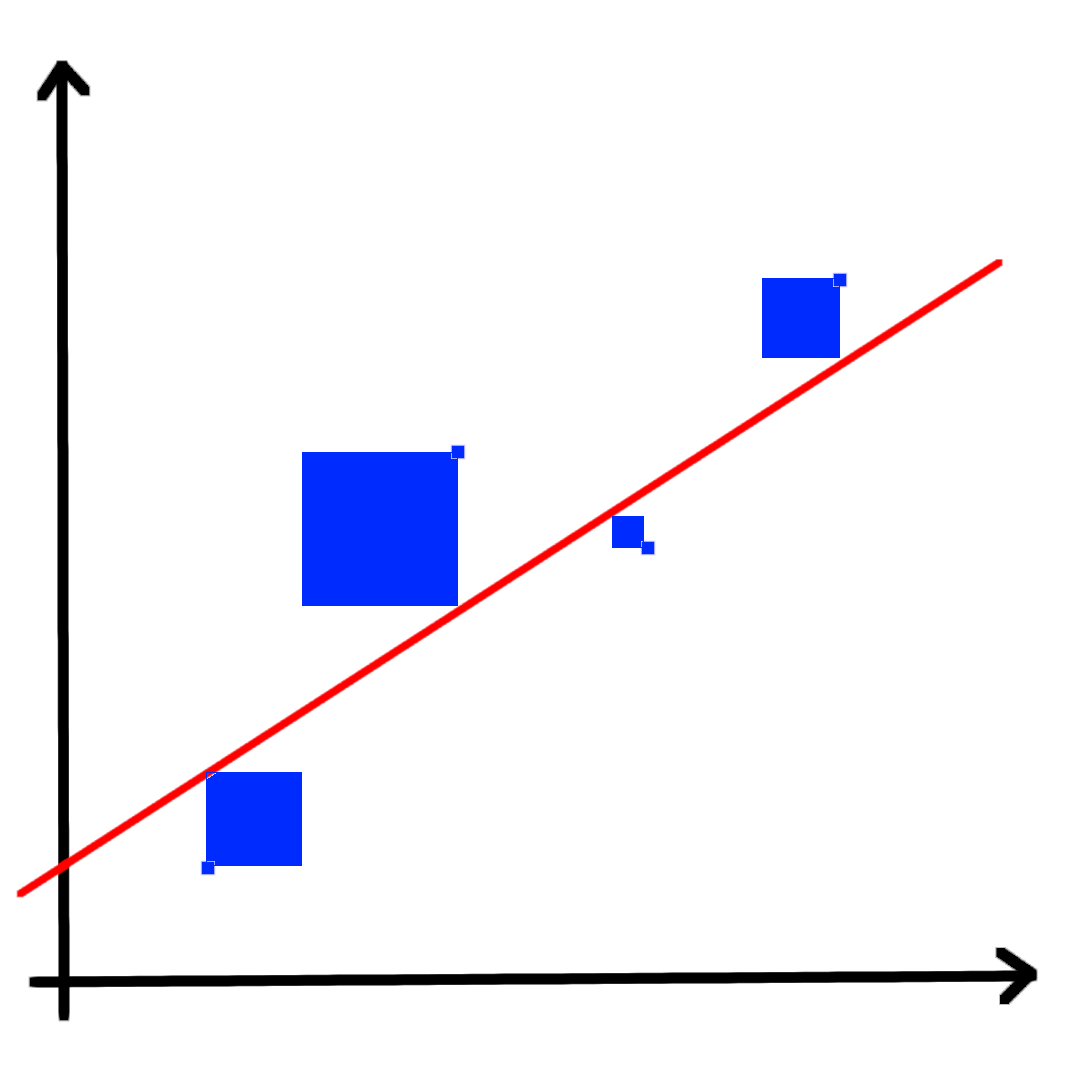
最小化误差平方的过程如上图所示，每个样本点的估计值与真实值的差的平方求和，即为蓝色区域部分面积总和。当直线使得面积总和最小时，直线即为最优解。

损失函数如下：

\[L(\theta) = \sum [y_i - (wx_i + b)]^2 \tag{1}\]

其中，\(\theta\)表示所有参数，直线用\(wx_i + b\)表示。当扩展到多项式时，还能够用最小二乘法吗？这个问题有点奇怪，因为一直以来我们总是习惯性地使用均方误差作为回归的损失函数，没有思考过背后有什么数学原理。当我们使用MSE的时候，本质上也是用了最小二乘法的思想，所以后文都对MSE做解释。下面是对回归问题中的均方误差损失的理解。

2. 充分必要条件

下面一步一步来思考：

我们观察到的数据总是受到误差的影响，同时假设这个误差\(\epsilon\)服从高斯分布（相当于假设整个数据集从高斯分布采样），可以把\(\epsilon\)服从的高斯分布认为是均值为0，方差为\(\sigma\)的高斯分布，即\(p(\epsilon) = N(0, \sigma^2)\)。真实的标签为\(y\)，我们估计结果为\(\hat y\)，那么不难得到：

\[y = \hat y + \epsilon \tag{2}\]

所以，整个数据集的分布就是均值为\(\hat y\)（或者说是观察到的\(y\)），方差为\(\sigma\)的高斯分布。即：

\[p(y|x) = N(y;\hat y, \sigma^2) \tag{3}\]

结论： 采用MSE的充分必要条件是： \(MSE / LSM \Longleftrightarrow p(\epsilon) = N(0, \sigma^2)\)

2.1 必要性

使用极大似然估计：

\[\begin{aligned} L(y_1, y_2, \cdots, y_n \vert x_1, x_2, \cdots, x_n) &= \prod_{i=1}^n p(y_i \vert x_i) \\ &= \prod_{i=1}^n N(y_i;\mu = \hat y_i, \sigma^2) \\ &= \prod_{i=1}^n \sqrt{\frac{1}{2 \pi \sigma^2}} \times \exp{(-\frac{1}{2 \sigma^2} (y_i - \hat y_i)^2)} \end{aligned} \tag{4}\]

对等式两边取对数：

\[\begin{aligned} \log L(y_1, y_2, \cdots, y_n \vert x_1, x_2, \cdots, x_n) &= \log (\prod_{i=1}^n \sqrt{\frac{1}{2 \pi \sigma^2}} \times \exp{(-\frac{1}{2 \sigma^2} (y_i - \hat y_i)^2)}) \\ &= \sum_{i=1}^n \log \sqrt{\frac{1}{2 \pi \sigma^2}} - \frac{1}{2 \sigma^2} (y_i - \hat y_i)^2 \\ \end{aligned} \tag{5}\]

移除掉与\(\hat y\)无关的项（\(\sigma\)），并取负数（最大化似然相当于最小化负似然）：

\[\begin{aligned} -L &= - \sum_{i=1}^n - \frac{1}{2} (y_i - \hat y_i)^2 \\ &= \frac{1}{2} \sum_{i=1}^n (y_i - \hat y_i)^2 \end{aligned} \tag{6}\]

可以得到：最大化似然，相当于最小化平方误差。所以必要性满足。

2.2 充分性

充分性要证明的问题是：如果采用了MSE并得到了最优参数，那么\(p(\epsilon) = N(0, \sigma^2)\)。

这一点的证明可以参考如何理解最小二乘法。

3. 重要前提

以上推理和证明都基于一个重要假设：假设这个误差\(\epsilon\)服从高斯分布（相当于假设整个数据集从高斯分布采样）。也就是第2节的第二行。

那么新的问题又出现了：现实数据中高斯分布常见吗？答案是肯定的，用一张网络上流传的趣图来表达这个意思吧。

相关思考

为什么MSE适用于回归，不适用于二分类问题？

参考

Why Using Mean Squared Error(MSE) Cost Function for Binary Classification is a Bad Idea?
Least squares
如何理解最小二乘法