Understanding Autograd and Dynamic Computation Graph
1. 前言
神经网络训练的核心方法是梯度下降,有手动实现过用梯度下降进行多项式回归的朋友一定都手动计算过参数的梯度,接着再用代码实现。PyTorch中的autograd包提供了对Tensor自动微分的功能,使得我们可以对大网络方便地进行梯度下降而无需任何手动计算。torch.Tensor是PyTorch表达数值的基本类型,其属性.requires_grad能够控制是否需要计算该张量的梯度,需要被更新的参数的这一项属性必须为True,否则参数将无法计算梯度,也就无法进行梯度下降更新。
>>> x = torch.zeros(1, requires_grad=True)
>>> y = x + 1
>>> y
tensor([1.], grad_fn=<AddBackward0>)
如上述代码所示,PyTorch会对追踪所有需要计算梯度的Tensor,记录他们被进行了什么操作(y是进行了Add操作而产生)。停止追踪的方法有两种:
- 执行.detach()函数能够抹去曾经记录的计算操作,并防止以后的操作被追踪。这个函数还将.requires_grad属性置为False;
- 对代码块包装:with torch.no_grad()。这个操作能在保持.requires_grad为True的情况下,被包装部分操作不需要计算梯度,节省显存空间。
2. Autograd
2.1 用法
PyTorch的Autograd模块使用非常简单,对某个Tensor执行.backward()函数,即可自动进行求导,为参数计算梯度。
>>> x = torch.ones(2, 2, requires_grad=True)
>>> y = x + 2
>>> z = y * y * 3
>>> o = z.mean()
>>> print(o)
tensor(27., grad_fn=<MeanBackward0>)
如上述代码所示,我们定义了参数\(x\),中间值\(y\),\(z\),\(o\)是被计算出来的,不是被定义出来的,所以他们不属于参数,Autograd不会计算他们的梯度,下面要获得\(x\)的梯度:
>>> o.backward()
>>> print(x.grad)
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
\(x\)的梯度被计算了出来。下面验证一下是否正确:
\[\begin{aligned} y &= x + 2 \\ z &= y * y * 3 \\ o &= \frac{1}{4} \sum_{i=1}^{4} z_i \end{aligned}\]利用链式法则(Chain rule):
\[\begin{aligned} \frac{\partial o}{\partial x_i} &= \frac{\partial o}{\partial z_i} \times \frac{\partial z_i}{\partial y_i} \times \frac{\partial y_i}{\partial x_i} \\ &= \frac{1}{4} \times 6 y_i \times 1 \\ &= \frac{9}{2} \\ &= 4.5 \end{aligned}\]从数学原理上理解,对于一个向量函数\(\vec y = f(\vec x)\),\(\vec y\)对于\(\vec x\)的梯度是一个雅可比矩阵:
\[J = \left[ \begin{matrix} \frac{\partial{y_1}}{\partial{x_1}} & \cdots &\frac{\partial{y_1}}{\partial{x_n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{y_m}}{\partial{x_1}} & \cdots &\frac{\partial{y_m}}{\partial{x_n}} \\ \end{matrix} \right]\]torch.autograd是一个能够计算雅可比矩阵乘法的工具,假设有另一个向量\(v = (v_1, v_2, \cdots, v_m)^T\),且\(v\)是标量函数\(l = g(\vec y)\)的梯度,那么 \(v = (\frac{\partial l}{\partial y_1} \cdots \frac{\partial l}{\partial y_m})^T\), 经过链式法则,\(l\)对于\(\vec x\)的梯度为:
\[J^T v = \left[ \begin{matrix} \frac{\partial{y_1}}{\partial{x_1}} & \cdots &\frac{\partial{y_m}}{\partial{x_1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{y_1}}{\partial{x_n}} & \cdots &\frac{\partial{y_m}}{\partial{x_n}} \\ \end{matrix} \right] \left[ \begin{matrix} \frac{\partial{l}}{\partial{y_1}} \\ \vdots \\ \frac{\partial{l}}{\partial{y_m}} \end{matrix} \right] = \left[ \begin{matrix} \frac{\partial{l}}{\partial{x_1}} \\ \vdots \\ \frac{\partial{l}}{\partial{x_n}} \end{matrix} \right]\]2.2 可视化
利用PyTorchvis工具对动态计算图进行可视化:
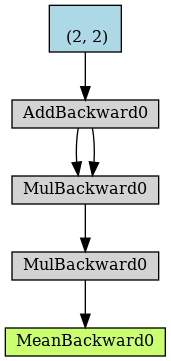
其中,蓝色块是叶子Tensor,autograd只会对叶子节点计算梯度,中间变量在计算完梯度后将会释放。
下面代码对两层卷积进行可视化:
model = nn.Sequential()
model.add_module('conv1', nn.Conv2d(1, 3, kernel_size=3, stride=2, padding=1))
model.add_module('conv2', nn.Conv2d(3, 12, kernel_size=3, stride=2, padding=1))
x = torch.randn(4, 1, 28, 28)
y = model(x)
y = y.mean()
torchviz.make_dot(y, params=dict(model.named_parameters()))
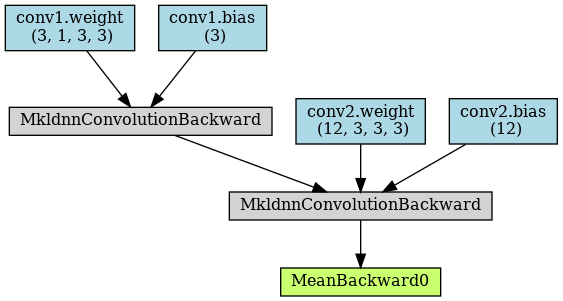
从上图可以看出:两层卷积conv1和conv2的参数weight和bias都出现在叶子节点,都会计算梯度。
如果我们将其中一层卷积的所有参数的.requires_grad属性置为False:
model = nn.Sequential()
model.add_module('conv1', nn.Conv2d(1, 3, kernel_size=3, stride=2, padding=1))
model.add_module('conv2', nn.Conv2d(3, 12, kernel_size=3, stride=2, padding=1))
for param in model.conv2.parameters():
param.requires_grad = False
x = torch.randn(4, 1, 28, 28)
y = model(x)
y = y.mean()
torchviz.make_dot(y, params=dict(model.named_parameters()))
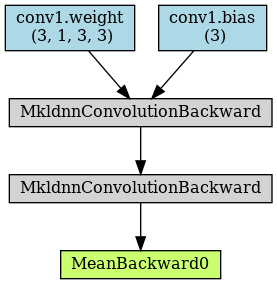
从上图可以看出:虽然卷积仍然进行,但是conv2的参数不再出现在叶子节点上,所以不会更新。
3. 动态计算图
目前神经网络框架分为静态图框架和动态图框架,代表分别为:Tensorflow和PyTorch。
3.1 静态计算图 vs. 动态计算图
Static:
- 静态图是在运行之前将图构建完成,每次运行的时候图都是一样的、不可改变的,所以不能用Python的while循环语句,需要辅助函数tf.while_loop写成Tensorflow的内部的形式;(缺点)
- 静态图不方便debug;(缺点)
- 定义好图后相当于建立好了整个流程,此时发现shape不match,运行之前就会报错;(优点)
- 静态图的框架会在运行之前帮助优化流程;(优点)
- 静态图是提前定义好的,再次运行不需要重新构建计算图,理论上来说速度比动态图更快。(优点)
Dynamic:
- 动态图每次迭代都重新构建计算图;(缺点)
- 动态图在运行forward函数时才能发现shape不match,可能运行了很长时间才发现自己粗心的写的bug;(缺点)
- 动态图的语法可以和Python完全一致,灵活方便;(优点)
Reference
autograd_tutorial
understanding pytorch
cs231n_2018_lecture08