Understanding the EM algorithm
1. 密度估计
假设现在要用密度估计(Density estimation)方法解决某异常检测(Anomaly detection)问题,现在有飞机引擎以抖动频率和温度为指标的数据,且无标签:
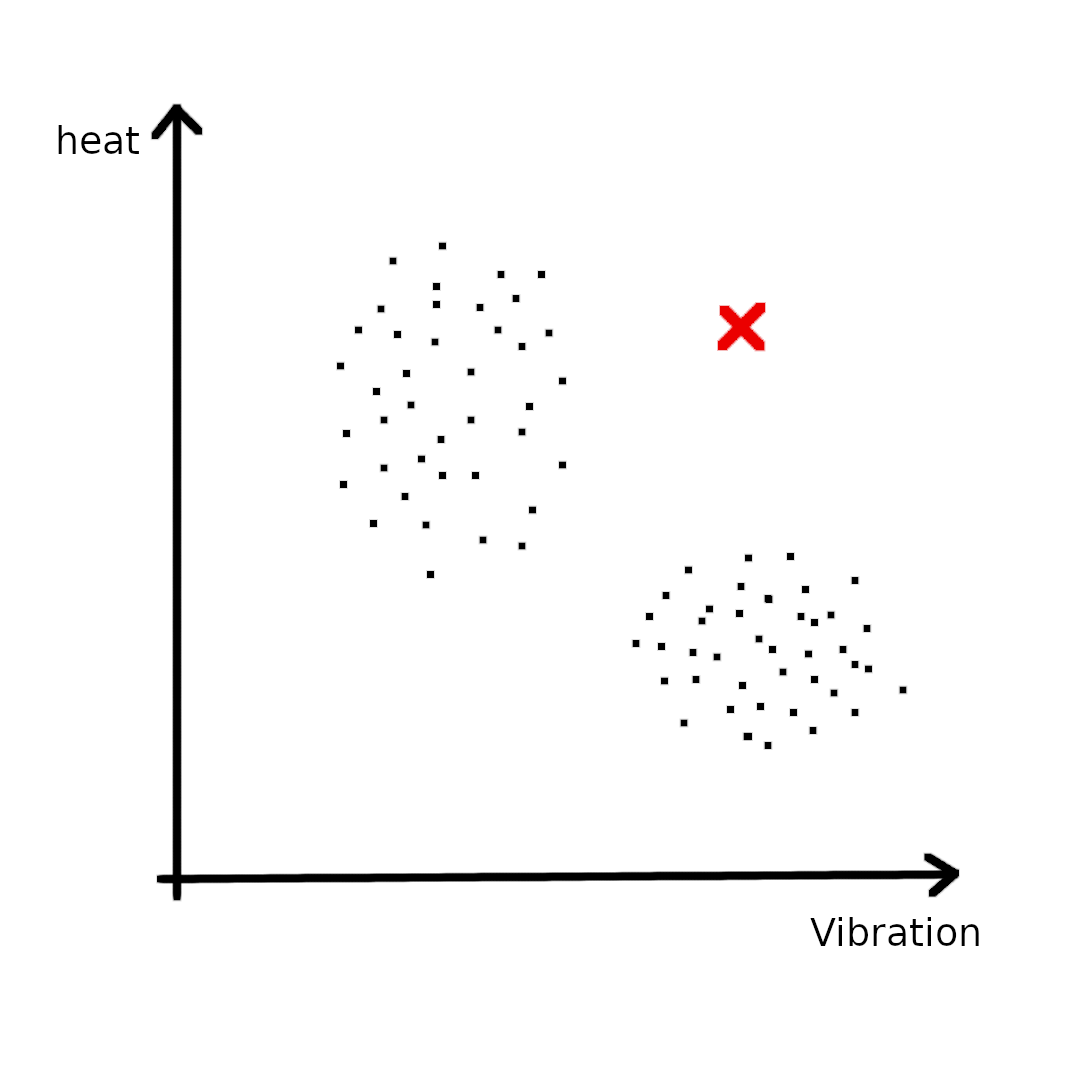
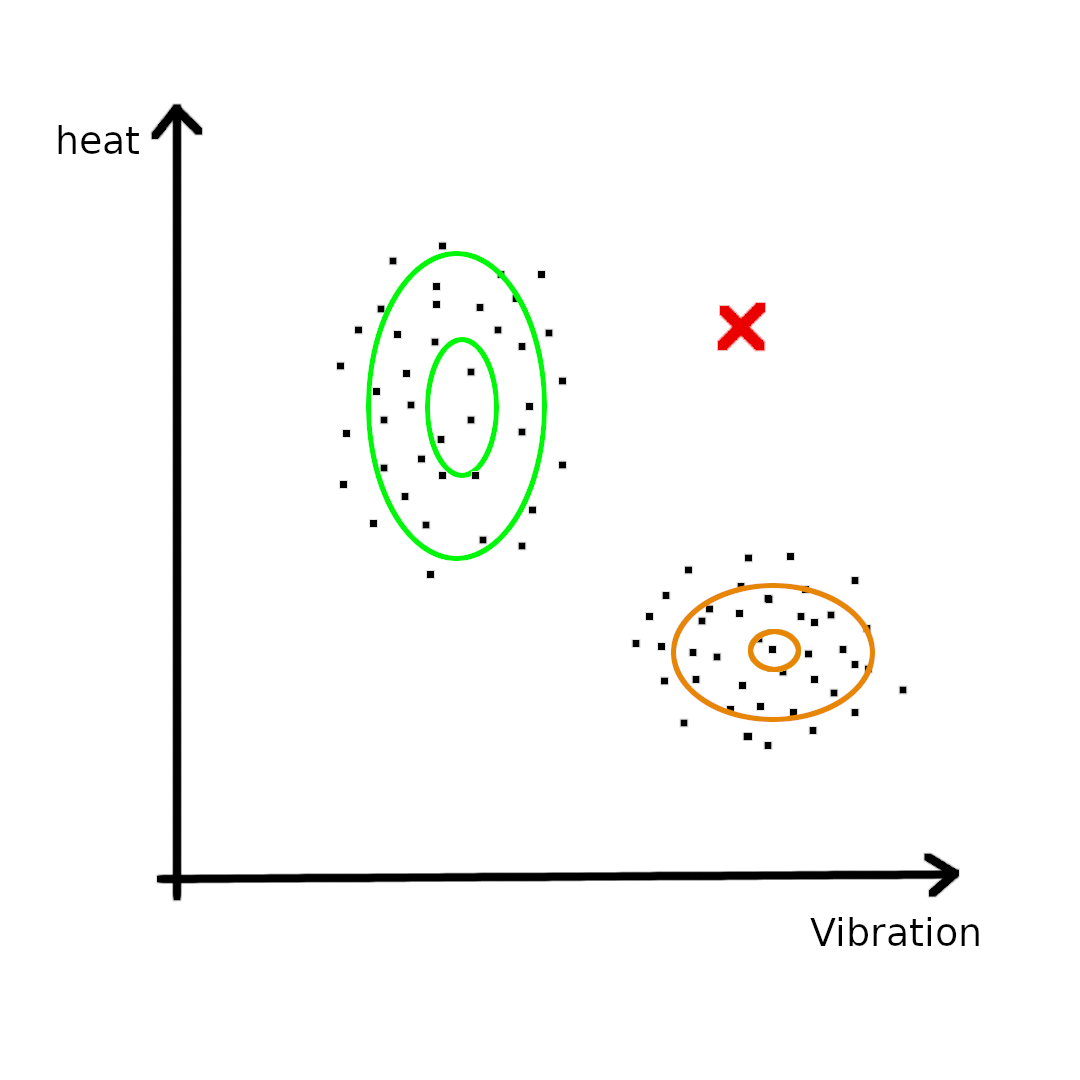
如上图(左)所示,收集的数据点在二维坐标中分布为两大块。此时请问当引擎的数据是红色点时,是否发生异常?显然我们会认为这个数据点很大可能有问题,虽然红点的Vibration和heat的取值各自都在合理范围内,但合在一起发生时却不符合规律。为了实现异常检测,我们建立概率模型\(p(x)\),表示事件\(x\)发生的概率,当\(p(x) > \epsilon\)时,我们认为正常,否则异常。
但有时候数据的分布很难直接与我们熟悉的分布重合,例如上述例子,数据点形成了类似“L”形的结构,没有任何一种概率分布能够直接表示它,所以这会用到高斯混合模型,把上述数据看成是两个高斯分布混合在一起的分布,如上图(右)所示。
1.1 高斯混合例子
假设已知数据分为两类,分别从两个高斯分布中采样出来:
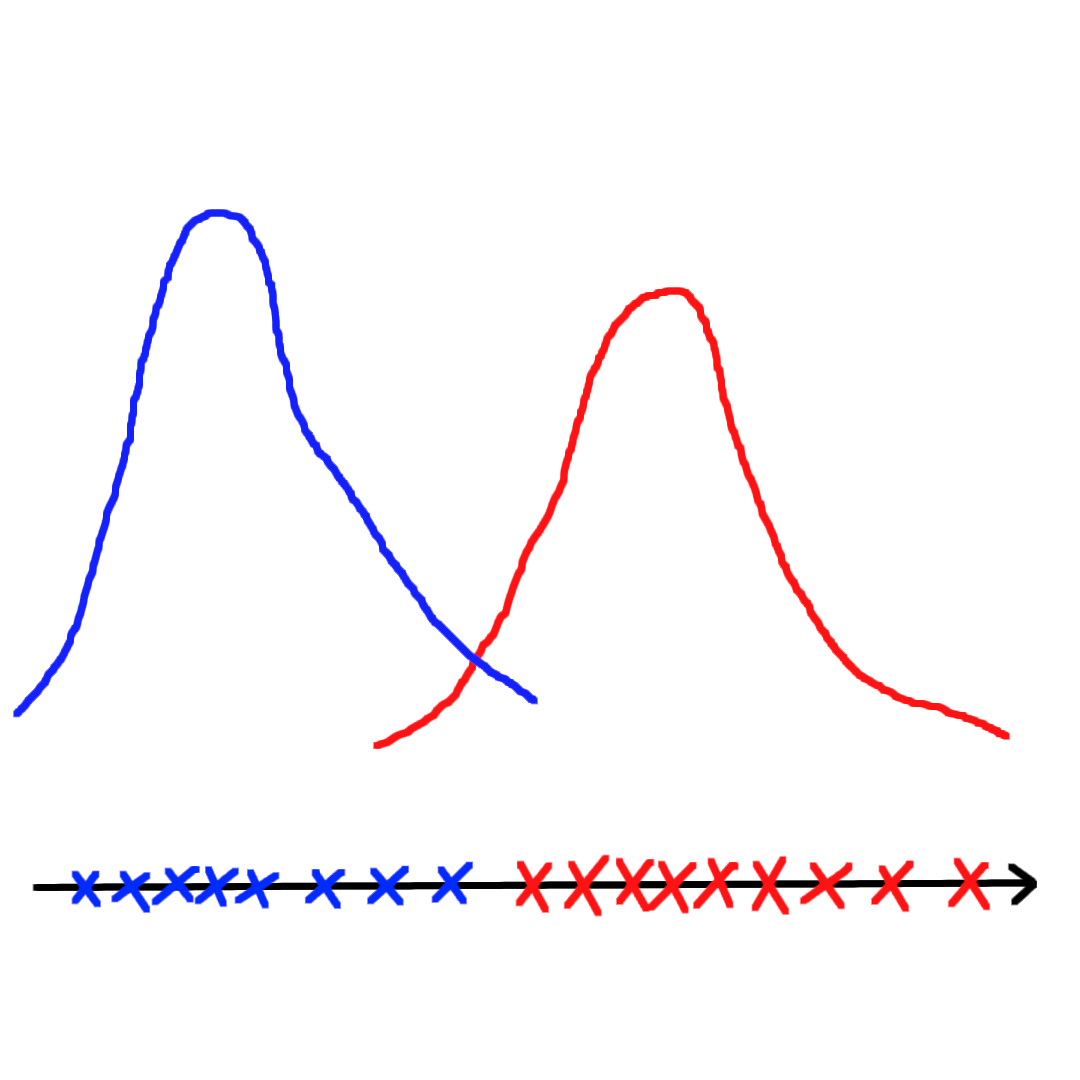
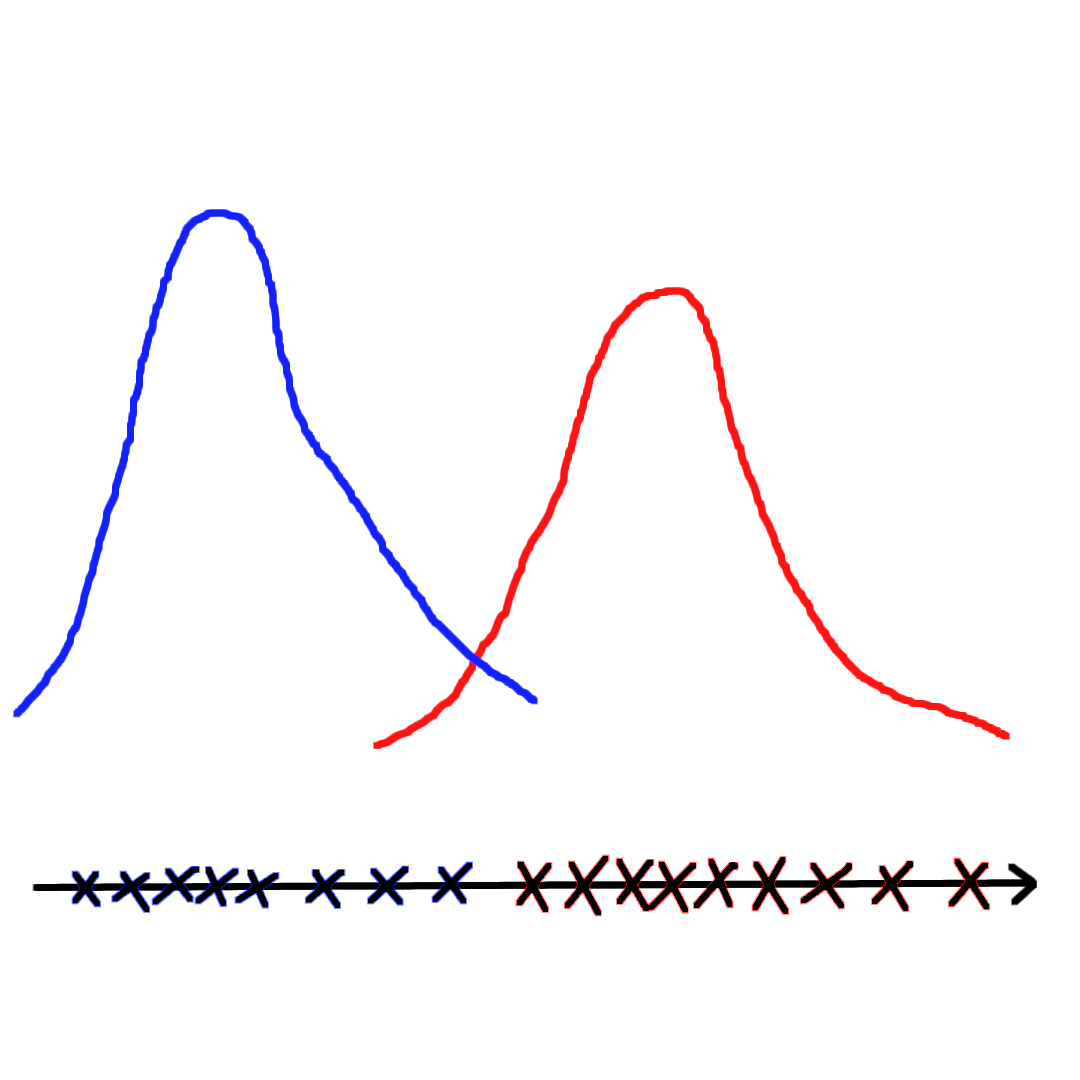
如上图(左)所示,如果给定数据点的标签,例如蓝色和红色各自为某个高斯分布中采样获得,这相当于监督学习问题,可以使用极大似然估计(MLE)方法直接对参数进行估计。如果将标签抹去,如上图(右)所示,只知道数据点的采样情况,那么是无法直接使用极大似然估计的,因为1. 无法确定一共有多少个分布;2. 无法确定每个样本分别来自哪个分布。但是我们能猜测这些数据来自两个高斯分布,接着使用一定的估计方法估计出参数。
1.2 实际场景
为了更深入理解EM算法的实际应用场景,下面再举一个例子:
假设一支球队进行比赛有主场、客场之分,每次选择一个场地连续打10次比赛:
| 场地 | 赛果 |
|---|---|
| 主场 | 8W2L |
| 客场 | 5W5L |
| 客场 | 4W6L |
| 主场 | 7W3L |
| 客场 | 6W4L |
显然上述过程有两个变量未知:1. 选择主场的概率;2. 主场、客场胜率。
但是数据中毕竟给出我们选择主场还是客场,相当于给了标签,所以先不关注第一个变量,可以用极大似然估计法(模型已定:伯努利分布,参数未知)算出主场、客场各自的胜率。
如果数据中没有主场、客场的数据呢?例如:
| 场地 | 赛果 |
|---|---|
| ? | 8W2L |
| ? | 5W5L |
| ? | 4W6L |
| ? | 7W3L |
| ? | 6W4L |
这时候场地信息相当于隐变量,我们不能知道它到底是什么,但它确实影响着结果。又比如给定身高预测体重的情景,这其中年龄、身体状况就可能是隐变量,因为数据中没有标注出来(搜集数据过程中没有被观察),但它确实有可能影响着结果。
2. 隐变量
理解隐变量(Latent variable)是理解EM算法的关键,上面总共举了三个例子是为了帮助理解隐变量在参数估计过程中的角色。它是不可知的、未被观察变量,与被观察的变量相对应。在异常检测和高斯混合的两个例子中,隐变量就是数据点属于哪个高斯分布;在篮球主场客场的例子中,隐变量就是比赛是在哪个场地进行。
假设存在数据\(\{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\}\),对每个样本有对应的隐变量\(\{z^{(1)}, z^{(2)}, \cdots, z^{(m)}\}\),那么有:
\[p(x^{(i)}, z^{(i)}) = p(x^{(i)} | z^{(i)}) p(z^{(i)}) \tag{2-1}\]3. EM算法
EM(Expectation–maximization)算法是一种通过迭代方式寻找局部最大似然(最大后验)的参数估计方法。模型依赖于假设存在未观察到的隐变量。
假设我们知道隐变量\(z^{(i)}\),那么可以使用极大似然估计:
\[l(\phi, \mu, \Sigma) = \sum_{i=1}^m \log p(x^{(i)}, z^{(i)}; \phi, \mu, \Sigma) \tag{3-1}\]其中,\(\phi\)表示选择各个高斯分布的概率,\(\mu\)和\(\Sigma\)表示各个高斯分布的均值和方差。对上式求偏导,获得各个参数的值。然而现实的数据大部分没有那么简单,在没有隐变量的情况下就要采用EM算法逐步优化得到参数值。EM算法的迭代分为两个步骤:Expectation步骤和Maximization步骤。
3.1 E-step
对隐变量\(z^{(i)}\)进行猜测:
\[\begin{aligned} w_j^{(i)} &= p(z^{(i)} = j \vert x^{(i)}; \phi, \mu, \Sigma) \\ &= \frac{p(x^{(i)} \vert z^{(i)} = j) p(z^{(i)} = j)}{\sum_{k=1}^m p(x^{(i)} \vert z^{(i)} = k) p(z^{(i)} = k)} \\ \end{aligned} \tag{3-2}\]上式只需要一步贝叶斯公式即可推出。其中\(w_j^{(i)}\)表示样本\(x^{(i)}\)是第\(j\)个高斯分布采样的程度。观察分子:\(p(x^{(i)} \vert z^{(i)} = j)\)理解为\(N(x^{(i)}; \mu_j, \Sigma_j)\),即将样本\(x^{(i)}\)代入第\(j\)个高斯分布的密度函数;\(p(z^{(i)} = j)\)理解为\(\phi_j\),即选择第\(j\)个高斯分布的概率。
注意:每个样本对每个分布都要计算一次\(w_j^{(i)}\)。
这里也可以看出EM算法与KMeans的相似性和差异性:
- KMeans会对每个样本计算到所有Centroids的距离;(相似)
- 但是KMeans对每个样本只会分配给离它最近的中心(Hard assignment),相当于以100%概率分配给某个中心;而EM则是保留每个样本产生于每个分布的概率(Soft assignment)。(差异)
3.2 M-step
利用猜测出来的隐变量,对式\((3-1)\)进行最大似然估计:
\[\phi_j = \frac{1}{m} \sum_{i=1}^m w_j^{(i)} \tag{3-3}\] \[\mu_j = \frac{\sum_{i=1}^m w_j^{(i)} x^{(i)}}{\sum_{i=1}^m w_j^{(i)}} \tag{3-4}\]4. 原理解析
总体来说,EM算法完成的工作是构建模型\(p(x, z; \theta)\):
\[\theta = \arg \min_{\theta} \prod_{i=1}^m p(x^{(i)}; \theta) \tag{4-1}\]其中,\(\theta\)表示模型参数如\(\mu\),\(\Sigma\)等等。
为什么按照EM算法的两个步骤就能够工作?怎么保证收敛性?下面是对EM算法背后数学原理的探讨。
4.1 数学基础
Jensen’s 不等式(Jensen’s inequality):
令\(f\)为凸函数(convex function),它有性质:\(f''(x) > 0\)。令\(x\)为随机变量,则如下不等式成立:
\[f(E[x]) \leqslant E[f(x)] \tag{4-2}\]Example:
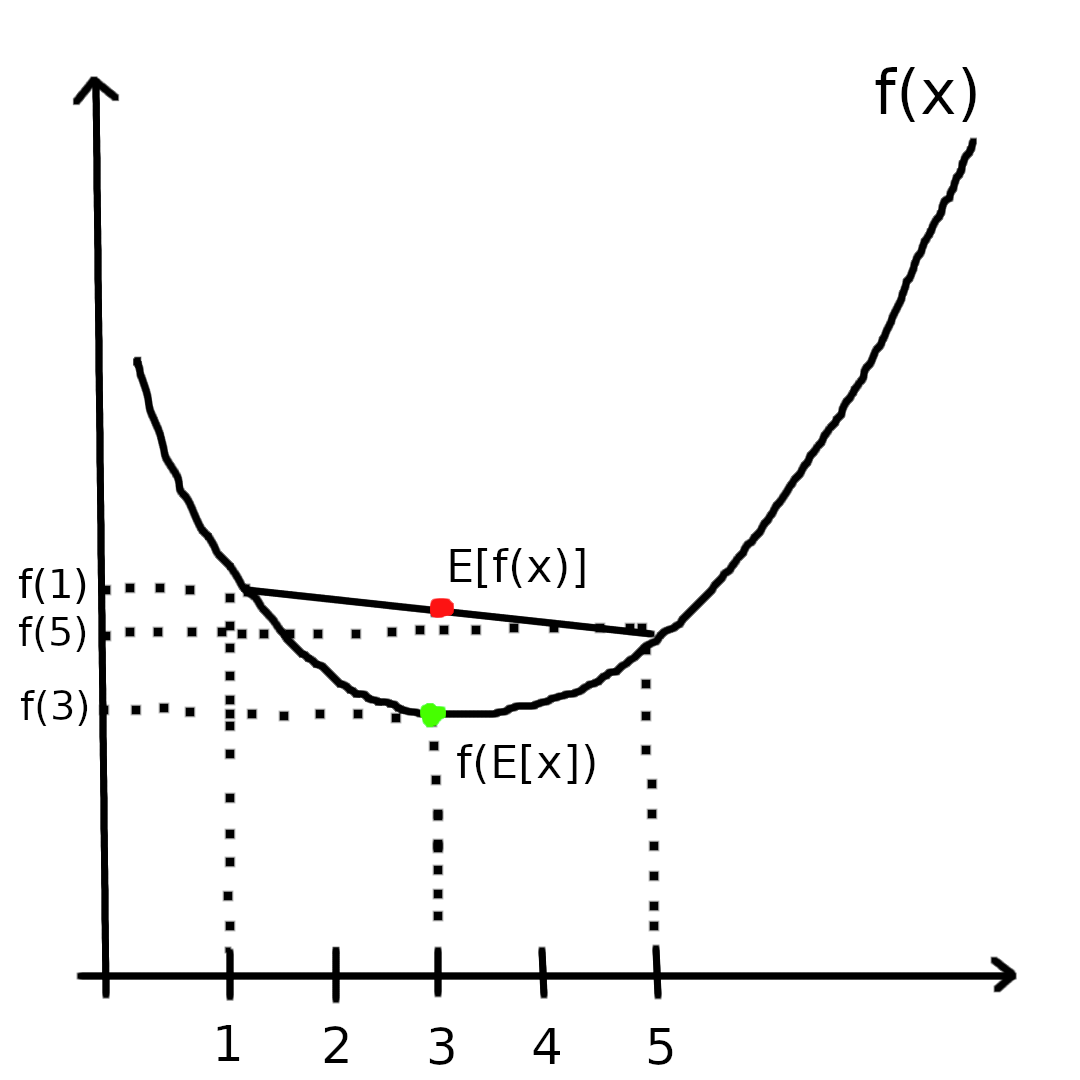
假设\(x=\{1, 5\}\),分别以\(\frac{1}{2}\)的概率等于1和5,那么\(E[x]=3\),\(E[f(x)] = \frac{1}{2}f(1) + \frac{1}{2}f(5)\),所以显然式\((4-2)\)不等式成立。
对于凸函数满足上述性质,而对于凹函数(concave function)的性质则只需要将上式的不等式符号转变即可:
\[f(E[x]) \geqslant E[f(x)] \tag{4-3}\]4.2 原理
问题描述:建立模型\(p(x, z; \theta)\),只观察到数据\(x=\{x^{(1)}, x^{(2)}, \cdots, x^{(m)}\}\),似然函数如下:
\[\begin{aligned} l(\theta) &= \sum_{i=1}^m \log p(x^{(i)}; \theta) \\ &= \sum_{i=1}^m \log \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) \end{aligned} \tag{4-4}\]Want:\(\arg \max_{\theta} l(\theta)\)
假设对于每个样本\(x^{(i)}\),令\(Q_i\)表示该样本隐含变量\(z\)的分布,\(Q_i\)满足\(\sum_{z^{(i)}} Q_i (z^{(i)}) = 1\),延续式\((4-4)\)可得:
\[\begin{aligned} l(\theta) &= \sum_{i=1}^m \log \sum_{z^{(i)}} Q_i(z^{(i)}) [\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}] \\ &= \sum_{i=1}^m \log E_{z^{(i)} \sim Q_i} [\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}] \\ &\geqslant \sum_{i=1}^m E_{z^{(i)} \sim Q_i} [\log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}] \\ &= \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \end{aligned} \tag{4-5}\]由于\(\log\)是凹函数,所以根据Jensen不等式可以推出式\((4-5)\)。式\((4-5)\)给出了对数似然函数的下界,此时假设已知\(\theta\)(初始时确实是随机初始化\(\theta\)),我们可以优化得到\(Q_i\),其中:
\[f(E_{z^{(i)} \sim Q_i} [\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}]) \geqslant E_{z^{(i)} \sim Q_i} [f(\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})})] \tag{4-6}\]为了使得不等式能够取等号,根据Jensen不等式,需要让随机变量的值为常数:
\[\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} = const \tag{4-7}\]由于\(Q_i\)函数满足\(\sum_{z^{(i)}} Q_i (z^{(i)}) = 1\),所以:
\[\sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) = \sum_{z^{(i)}} cQ_i(z^{(i)}) = c \tag{4-8}\]将式\((4-8)\)代入式\((4-7)\),可得:
\[\begin{aligned} Q_i(z^{(i)}) &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{\sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta)} \\ &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{p(x^{(i)}; \theta)} \\ &= p(z^{(i)} \vert x^{(i)}; \theta) \end{aligned} \tag{4-9}\]观察此式,是否与式\((3-2)\)一模一样。该式能计算出\(Q_i\)的后验概率分布,以上为E-step过程。而M-step过程就是固定计算出来的\(Q_i\)优化\(\theta\)。
4.3 可视化
EM算法的整体过程是不断构建似然函数的下界,寻找局部最优值的迭代过程:
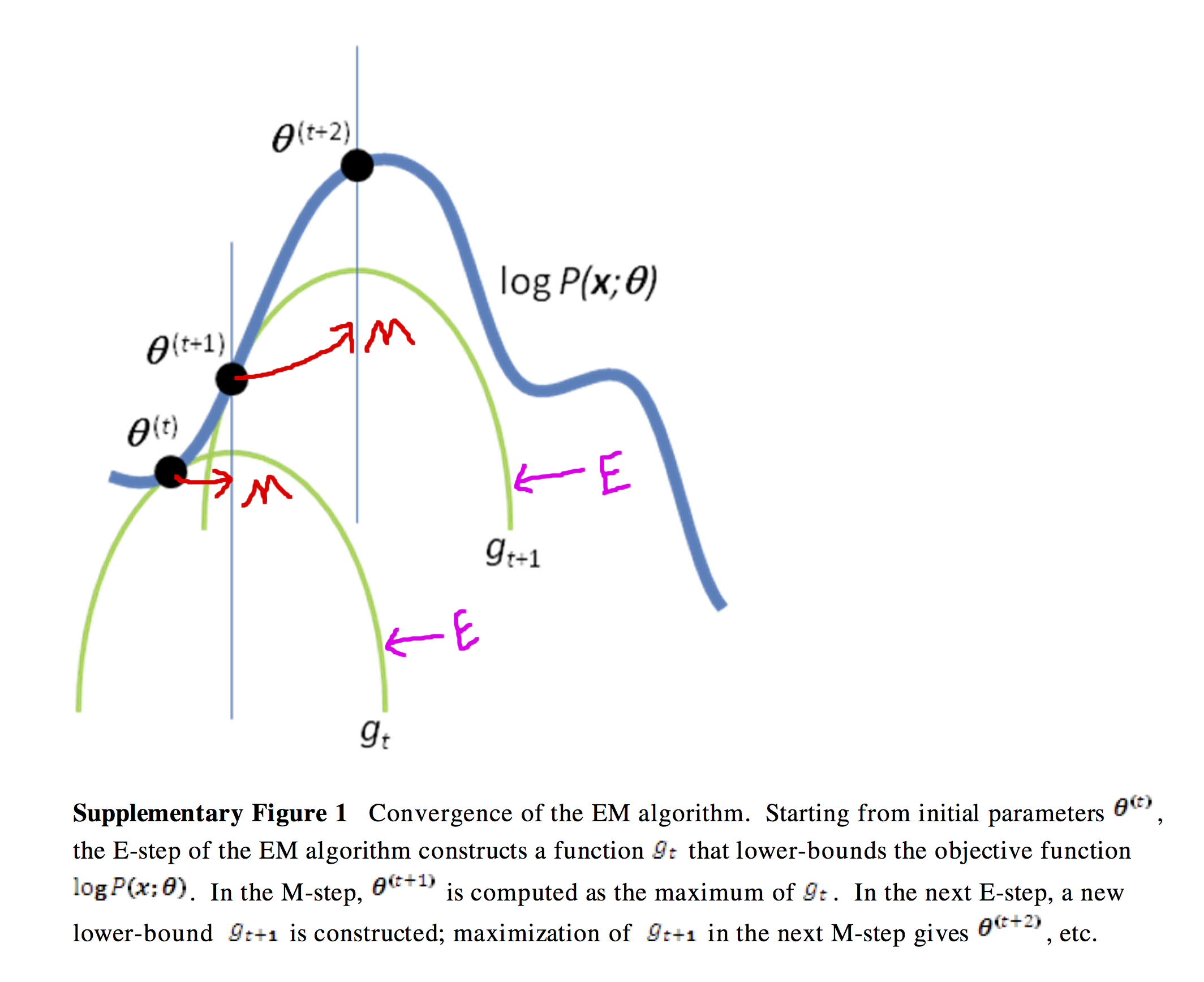
- E-step:Construct the lower bound
- M-step:Find the local maximization
其中,绿色曲线是E-step构建出来的优化下界,M-step则寻找到局部最优值。不断循环迭代下去,算法最终能够寻找到一个局部最优值(不是全局最优),所以为了避免EM陷入局部最优,可以在随机初始化的基础上多运行几次算法。
5. 总结
Radnom initialization \(\theta\)
repeat untial convergence:
- E-step: For each \(x^{(i)}\), set \(Q_i(z^{(i)}) = p(z^{(i)} \vert x^{(i)}; \theta)\)
- M-step: \(\theta = \arg \max_{\theta} = \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}\)
参考
Stanford CS229: Machine Learning
Expectation Maximizatio (EM) Algorithm
EM算法