Understanding the Linear Discriminant Analysis
1. 线性判别的概念
线性判别分析(Linear Dscriminant Analysis)可以简写为LDA,是一种监督学习的维度归约和分类的方法。在自然语言处理领域也有一种LDA:Latent Dirichlet Allocation,隐含狄利克雷分布,但本文讲述的是前者。
假设特征空间为二维空间,对于特征空间中的数据,我们希望找到空间中一条线(向量),数据在这条线上的投影则是一种归约。归约后的数据自然地分隔开了,那么就可能够进行分类。其过程如下图所示:
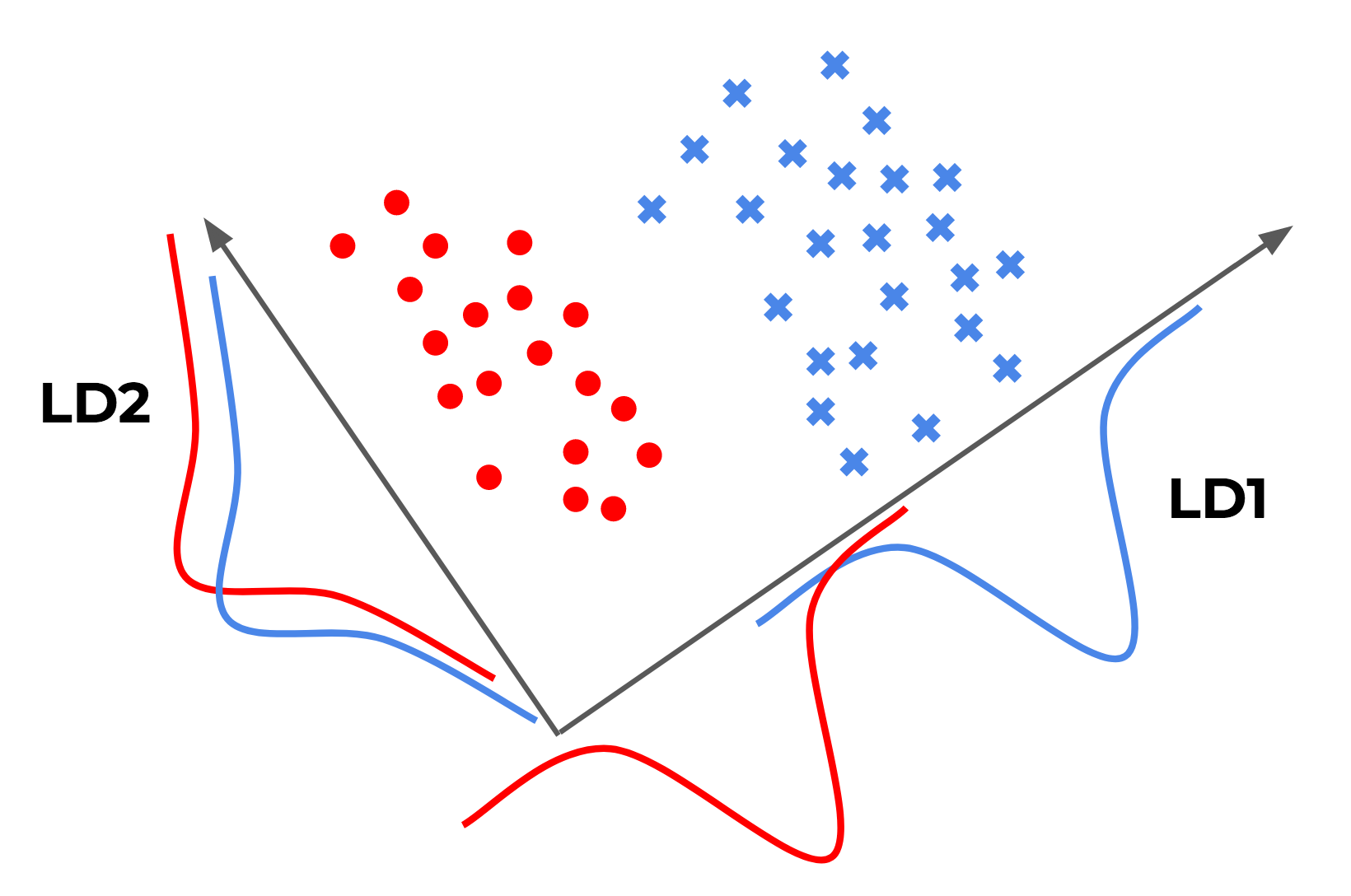
图中有两条直线,红点与蓝点在分别投影在它们上,显然投影后LD1的效果比LD2的效果更好,数据分隔更开。
2. 理解误区——投影
我在学习LDA的时候难以理解“投影”这个过程,一个点到一条线的投影要怎么表示?
我们知道一个点可以用向量来表示:\(\vec{u}\),将空间中的一条直线也用向量来表示:\(\vec{v}\),假设他们的夹角为\(\theta\)。那么\(\vec{u}\)在\(\vec{v}\)上的投影为:\(\vert \vec{u} \vert \cos \theta\),\(\vec{v}\)在\(\vec{u}\)上的投影为:\(\vert \vec{v} \vert \cos \theta\)。
但是我们在计算的时候不能总是轻松获得夹角\(\theta\),我们求助于另外一个概念:点积(Dot product)。
\[\begin{aligned} \vec{u} \bullet \vec{v} &= \vert \vec{u} \vert \times \vert \vec{v} \vert \times \cos \theta \\ &= u_1 * v_1 + u_2 * v_2 + \cdots + u_n * v_n \end{aligned} \tag{2-1}\]其中\(n\)表示空间维度。可以认为:这是点在直线上投影后扩大\(\vert \vec{v} \vert\)倍。也可以认为:这是点的特征带权重的线性组合。
网上很多教程把\(\vec{u} \bullet \vec{v}\)直接说成是“投影”,我认为这不太准确。它一定程度表示投影,但不等同于投影。后文中会继续使用“投影”的概念,这里要理解清楚。
基于上述理解,LDA模型最终要得到什么?如果是第一个粗体字的理解,那么我们是寻找找一条直线;如果是第二个粗体字的理解,那么我们是在寻找一个权重向量。
3. 符号约定
给定数据集\(D = \{(x_i, y_i)\}_{i=1}^m\),其中任意样本\(x_i\)为\(n\)维向量,令\(N_i\)和\(X_i\)分别表示第\(i\)类的样本数量和样本集合。
用向量\(w\)表示要求的直线,对于任意一个样本\(x_i\),在直线上的投影为\(w^{\top}x\)。
4. 二分类
我们希望投影后的数据尽可能满足两个条件:
- 类内的方差尽可能小;
- 类间的方差尽可能大。
定义\(\mu_i\)为第\(i\)类的均值点(将全部特征求均值):
\[\mu_i = \frac{1}{N_i} \sum_{x \in X_i} x \tag{4-1}\]为满足第二个条件,使得各类的均值点投影后尽可能分开:
\[\arg \max_{w} J(w) = |w^{\top} \mu_1 - w^{\top} \mu_2|^2 \tag{4-2}\]定义\(\Sigma_i\)为第\(i\)类的类内方差(省略取均值过程):
\[\Sigma_i = \sum_{x \in X_i} (w^{\top}x - w^{\top}\mu_i)^2 \tag{4-3}\]为满足第一个条件,使得各类样本尽可能聚集:
\[\arg \max_{w} J(w) = \frac{|w^{\top} \mu_1 - w^{\top} \mu_2|^2}{\Sigma_1 + \Sigma_2} \tag{4-4}\]将类内方差展开:
\[\Sigma_i = \sum_{x \in X_i} (w^{\top}x - w^{\top}\mu_i)^2 = \sum_{x \in X_i} w^{\top} (x-\mu_i) (x-\mu_i)^{\top} w \tag{4-5}\]其中,定义:
\[S_i = \sum_{x \in X_i} (x-\mu_i) (x-\mu_i)^{\top} \tag{4-6}\]\(S_i\)是去掉了均值操作的协方差矩阵,称为散列矩阵(Scatter matrix),定义类内散列矩阵(Within-class scatter matrix)为\(S_W\):
\[S_W = \sum_{i} S_i \tag{4-7}\]同样将分子展开:
\[|w^{\top} \mu_1 - w^{\top} \mu_2|^2 = w^{\top} (\mu_1 - \mu_2) (\mu_1 - \mu_2)^{\top} w \tag{4-8}\]定义类间散列矩阵(Between-class scatter matrix)为\(S_B\):
\[S_B = (\mu_1 - \mu_2) (\mu_1 - \mu_2)^{\top} \tag{4-9}\]将式\((4-7)\)和\((4-9)\)代入\((4-4)\):
\[\arg \max_w J(w) = \frac{w^{\top} S_B w}{w^{\top} S_W w} \tag{4-10}\]在求极值之前还要做一件事情:由于我们用向量表示直线,但实际上向量有长度,直线是没有长度的,而且投影的大小与方向有关,与长度无关。所以,不失一般性,令\(w^{\top}S_Ww = 1\),则式\((4-10)\)变成有约束的优化问题,加入拉格朗日乘子并求导:
\[\begin{aligned} c(w) &= -w^{\top} S_B w + \lambda (w^{\top}S_W w - 1) \\ &\Rightarrow \frac{\partial c}{\partial w} = -2 S_B w + 2 \lambda S_W w = 0 \\ &\Rightarrow S_B w = \lambda S_W w \\ &\Rightarrow S_W^{-1} S_B w = \lambda w \end{aligned} \tag{4-11}\]此时注意到式\((4-9)\),则:
\[S_B w = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^{\top} w = (\mu_1 - \mu_2) * \lambda_w \tag{4-12}\]可以理解为:对\((\mu_1 - \mu_2)\)放缩\(\lambda_w\)倍,则:
\[S_W^{-1} S_B w = S_W^{-1} (\mu_1 - \mu_2) * \lambda_w = \lambda w \tag{4-13}\]由于放缩\(w\)不影响结果,所以约去\(\lambda_w\)和\(\lambda\),最终得到:
\[w = S_W^{-1} (\mu_1 - \mu_2) \tag{4-14}\]只需要求出原始样本的均值和方差就能够得到最优直线(向量)\(w\)。
5. 多分类
假设为\(k\)分类问题,当多类向低维投影时,此时投影的低维空间不一是直线,而是超平面。假设投影到的低维空间为\(d\),基向量组成的矩阵为\(W\),大小为\(n \times d\)。
优化目标为:
\[\arg \max_{W} J(W) = \frac{W^{\top} S_B W}{W^{\top} S_W W} \tag{5-1}\]其中,\(S_B = \sum_{j=1}^k N_j (\mu_j - \mu) (\mu_j - \mu)^{\top}\),\(\mu\)为所有样本均值向量。\(S_W = \sum_{j=1}^k S_{Wj} = \sum_{j=1}^k \sum_{x \in X_j} (x - \mu_j) (x - \mu_j)^{\top}\)
具体求解过程较为复杂,可移步到参考文献中查阅具体步骤。
6. LDA算法流程
输入:数据集\(D = \{(x_1, y_1), (x_2, y_2), \cdots, (x_m, y_m)\}\),其中任意样本\(x_i\)的维度为\(n\),\(y_i \in \{C_1, C_2, \cdots, C_k\}\),降维到\(d\)维。
- 计算类内散度矩阵\(S_W\)
- 计算类间散度矩阵\(S_B\)
- 计算矩阵\(S_W^{-1}S_B\)
- 计算\(S_W^{-1}S_B\)的最大的\(d\)个特征值和对应的\(d\)个特征向量\((w_1, w_2, \cdots, w_d)\),得到投影矩阵\(W\)
- 对每个样本\(x_i\),计算投影后的新样本\(z_i = W^{\top} x_i\)
参考
Linear Discriminant Analysis for Starters
线性判别分析LDA原理总结
线性判别分析LDA详解