1. 前言

之前遇到一个小问题上网搜索了关于整型二进制原码、反码和补码的问题，网上许多总结都很差劲。后来阅读了《深入理解计算机系统》第二章后，对这些概念有了更深入的认识，于是总结一下整型的二进制表示的方法。

2. 二进制表示

我认为，抛开整型类型去讨论二进制表示就是耍流氓。比如问：\(1000 \ 0000 \ 0000 \ 0000\)表示什么数？这是无法给出一个确定答案的。如果是short类型，那么是-32768；如果是unsigned short，那么是32768。(为什么？看完这篇总结就会有答案。)

2.1 整型类型

下面直接给出32位和64位系统下常见类型的表示范围（可能根据操作系统、编译器不同而变化）：

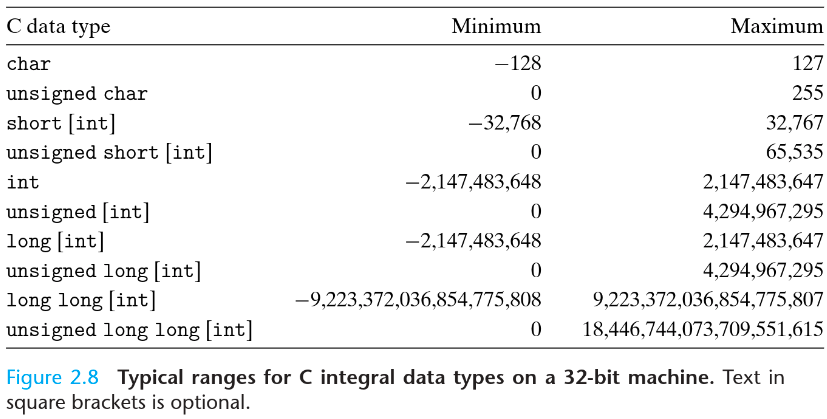
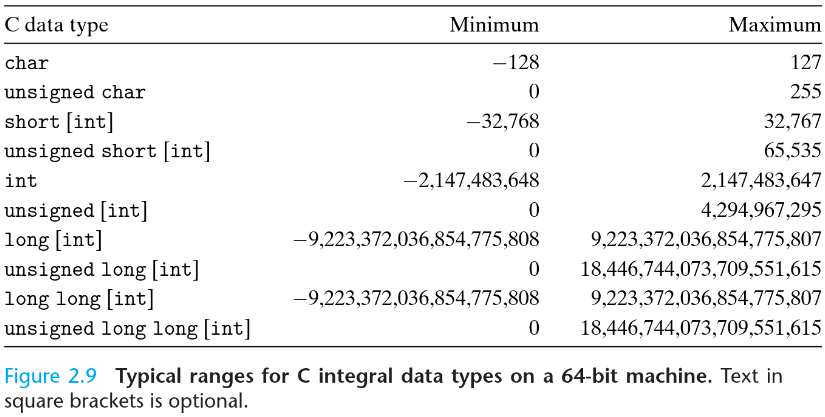
可以看出，常用的short类型是16位的，int类型是32位的。

2.2 正负数范围

以int为例，假如是unsigned int（无符号整型），则最大表示\(2^{31} + 2^{30} + \cdots + 2^1 + 2^0\)，即\(2^{32}-1\)：

\[\underbrace{1111 \ 1111 \cdots \ 1111 \ 1111}_{共32位}\]

因为无正负符号，所以不需要考虑其他因素，直接计算即可。

那么假如是int（有符号整型）呢？那么会把最高位作为符号位（1表示负数，0表示正数），就导致了int类型表示范围为：

\[-2^{31} \leq x \leq 2^{31}-1\]

更直观地看：

\[\underbrace{1或0}_{符号位} \underbrace{111 \ 1111 \ \cdots 1111 \ 1111}_{共31位}\]

当数值为：

\[\underbrace{0}_{符号位} \underbrace{111 \ 1111 \ \cdots 1111 \ 1111}_{共31位}\]

符号为0表示正数，结果为\(+2^{31} - 1\)。

当数值为：

\[\underbrace{1}_{符号位} \underbrace{111 \ 1111 \ \cdots 1111 \ 1111}_{共31位}\]

符号为1表示负数，结果为\(-(2^{31} - 1)\)。

这时候就会遇到一个疑问：为什么最小值为\(-(2^{31} - 1)\)？不是说好的\(2^{31}\)吗？

国内的教材、论坛会告诉你：因为当除了符号位以外的值都为0时，符号位的变化会导致出现\(+0\)和\(-0\)，他们俩存在一个就够了，所以规定\(-0\)为\(-2^{31}\)。于是int类型能够表示的最小值与最大值不一样。

以上对int类型范围的理解不是特别直观，个人不喜欢这样去理解二进制。

3. 原码、反码和补码

原码：二进制表示；

反码：除了符号位，其他位置取反；

补码：反码加一；

计算机存储所有数为补码，规定：正数的补码与原码相同，负数的补码是其反码加一。

例如，在讨论计算机存储时：

5的原码：0000 0101

5的补码：0000 0101

-5的原码：1000 0101

-5的补码：1111 1011 （取反加一）

4. 负数二进制更好的理解

“取反加一”来进行原码、补码转换的理解方式有点落后，因为在这种思考方式之下，当想要知道某个负数在计算机二进制中的表示时，还要先写出原码，取反，再加一逐个进位；当给一个负数的补码，想知道这个数是什么的时候，还要减一再取反，整个过程太不直观了。在阅读了《深入理解计算机系统》后，发现书中给出的理解方式更直观，直接定义补码（书中名为Two’s-Complement Encodings）：

对于一个数\(\overrightarrow{x} = [x_{w-1}, x_{w-2}, \cdots, x_0]\)

\[B2T_w(\overrightarrow{x}) = -x_{w-1} 2^{w-1} + \sum_{i=0}^{w-2} x_i 2^i \tag{1}\]

这个定义下，把符号位变为负数，其他位仍然为正数。例如：

\[\underbrace{1000 \ 0000 \ \cdots \ 0000 \ 0110}_{共32位}\]

它表示的负数为：\(-2^{31} + 2^2 + 2^1 = −2147483642\)

有一道算法题是计算一个整型包含多少个1，尝试一下把上面这个数放进去算一下，答案会是3。这也证明了计算机是存储二进制数的补码。

下面再尝试直接用补码去理解int类型的范围：

最大值：

\[\underbrace{0111 \ 1111 \ \cdots \ 1111 \ 1111}_{共32位}\]

即为\(2^{31} - 1\)。

最小值：

\[\underbrace{1000 \ 0000 \ \cdots \ 0000 \ 0000}_{共32位}\]

即为\(-2^{31}\)。

负数的最大值：

\[\underbrace{1111 \ 1111 \ \cdots \ 1111 \ 1111}_{共32位}\]

即为\(-2^{31} + 2^{30} + \cdots + 2^1 + 2^0 = -1\)

此时就不存在去理解\(+0\)和\(-0\)的问题，这样去理解int类型范围更直观。