Laplace's Method and its Application
1. 前言
拉普拉斯方法(Laplace’s method)由Pierre-Simon Laplace提出,该方法是一种特殊的积分情形下的近似解法。本文对Laplace’s方法的公式进行推导,并且简单验证它的两个应用(积分估计,斯图灵公式)。
2. 公式推导
目前要进行如下形式的定积分的计算:
\[\int_a^b e^{Mf(x)} dx \tag{1}\]显然是没有办法直接进行推导来计算积分,所以只能通过估计方法来计算积分结果。
现在考虑如下特殊情形:\(M \gg 0\) ,且\(f(x)\)在定义域仅存在一个极大值点,设为\(x_0\)。
对\(f(x)\)在\(x_0\)处进行二阶泰勒展开:
\[f(x) \approx f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2}(x-x_0)^2 \tag{2}\]由于\(x_0\)是极大值点,所以\(f'(x_0) = 0\),且\(f''(x_0) < 0\),所以上式可以写成:
\[f(x) \approx f(x_0) - \frac{\vert f''(x_0) \vert}{2}(x-x_0)^2 \tag{3}\]将式\((3)\)代入式\((1)\),得到:
\[\int_a^b e^{Mf(x)} dx \approx \int_a^b e^{M[f(x_0) - \frac{\vert f''(x_0) \vert}{2}(x-x_0)^2]} dx \tag{4}\]此时可以进行两个合理的假设:
- \(x_0 \in (a, b)\);
- 由于\(M\)非常大,\(x_0\)附近的积分贡献了整体积分的绝大部分,所以对\((a, b)\)进行积分约等于对\((-\infty, \infty)\)进行积分。
对于第2点假设的理解如下(图片来源):
其中,蓝线表示\(f(x)\),且在\(x_0=0\)时取极大值。在上图中\(M\)为一个比较小的值,下图中\(M\)为较大的值。可以看到,当\(M\)足够大时,\(x_0\)附近的积分对整体的积分贡献很大。所以当\(M \rightarrow \infty\)时,对\((a,b)\)的积分约等于对\((-\infty, \infty)\)。
因此,式\((4)\)可以写成:
\[\begin{aligned} \int_a^b e^{Mf(x)} dx &\approx \int_{-\infty}^{\infty} e^{M[f(x_0) - \frac{\vert f''(x_0) \vert}{2}(x-x_0)^2]} dx \\ &= e^{Mf(x_0)} \times \int_{-\infty}^{\infty} e^{-M\vert f''(x_0) \vert} \frac{(x-x_0)^2}{2} dx \\ &= \sqrt{\frac{2\pi}{M \vert f''(x_0) \vert}} \times e^{Mf(x_0)} \end{aligned} \tag{5}\]最终我们得到了对式\((1)\)的估计,这个方法叫做Laplace’s方法:
\[\int_a^b e^{Mf(x)} dx \approx \sqrt{\frac{2\pi}{M \vert f''(x_0) \vert}} \times e^{Mf(x_0)} \tag{6}\]当\(M \rightarrow \infty\),且\(x_0\)为唯一的极大值点。本质上是使用高斯分布的概率密度函数来估计\(Mf(x)\)的过程。
3. 应用
3.1 积分估计
举个例子,令\(f(x) = -x^2+x\),\(g(x) = e^{Mf(x)}\),易得\(f(x)\)的极大值点\(x_0\)为\(\frac{1}{2}\),并计算\(g(x)\)在\((0, 1)\)上的积分,以上条件都满足上述公式推导中的特殊情况。
依据式\((6)\)可以得到:
\[\int_0^1 e^{M(-x^2+x)} dx \approx \sqrt{\frac{\pi}{M}} \times e^{M(-x_0^2+x_0)} = \sqrt{\frac{\pi}{M}} \times e^{M/4} \tag{7}\]利用scipy.integrate库的函数来计算原函数的积分:
from scipy import integrate
import numpy as np
def func(x):
'''
e^{M*(-x^2+x)}
'''
return np.exp(M*(-x*x+x))
for i in [1, 10, 100, 1000]:
M = i
v, err = integrate.quad(func, 0, 1) # intergrate from 0 to 1
print(f'M = {i:4}, result = {v:10}')
得到输出结果:
M = 1, result = 1.1845930729386531
M = 10, result = 6.655198647053357
M = 100, result = 12762536111.441746
M = 1000, result = 2.099884520692089e+107
利用Laplace’s方法估计:
def approx(M):
'''
\sqrt{\frac{\pi}{M}} \times e^{M/4}
'''
return np.sqrt(np.pi/M)*np.exp(M/4)
for i in [1, 10, 100, 1000]:
res = approx(i)
print(f'M = {i:4}, result = {res:10}')
得到输出结果:
M = 1, result = 2.275875794468747
M = 10, result = 6.828277164356378
M = 100, result = 12762536111.461365
M = 1000, result = 2.0998845206920974e+107
可以得到:
| M | 原函数定积分 | 拉普拉斯估计 | 误差(%) |
|---|---|---|---|
| 1 | 1.1845930729386531 | 2.275875794468747 | 47.95 |
| 10 | 6.655198647053357 | 6.828277164356378 | 2.53 |
| 100 | 12762536111.441746 | 12762536111.461365 | 0.00 |
| 1000 | 2.099884520692089e+107 | 2.0998845206920974e+107 | 0.00 |
当\(M\)的值越来越大,Laplace’s方法估计的结果越准确。
以下是函数的可视化:
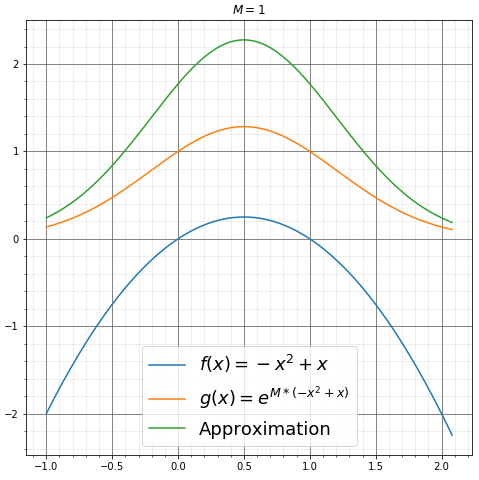
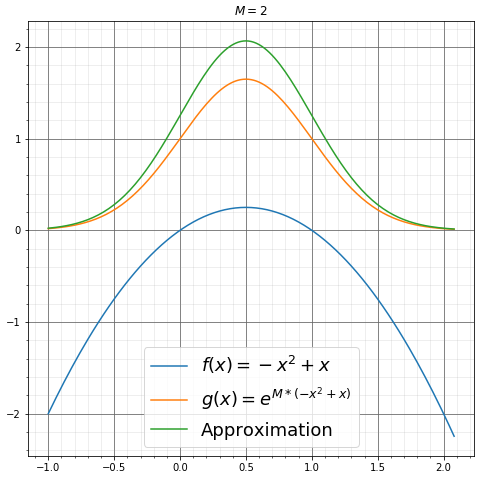
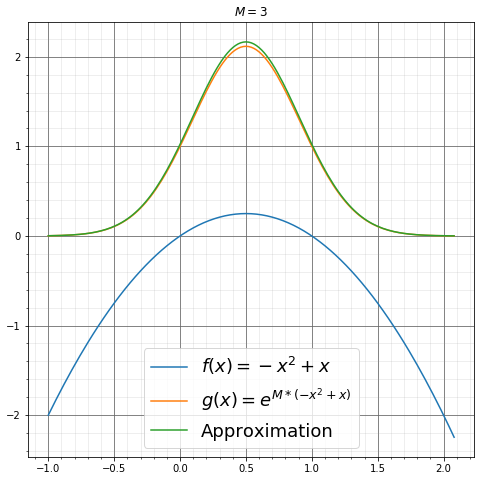
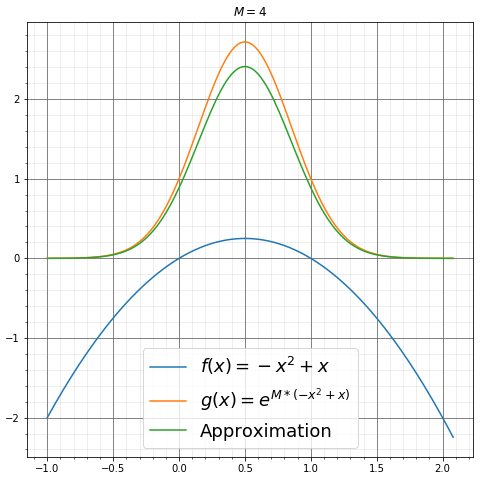
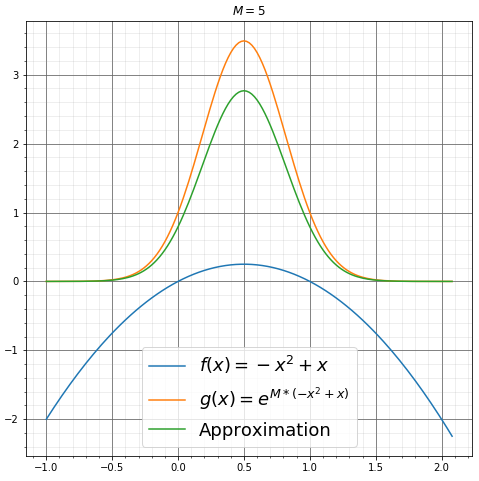
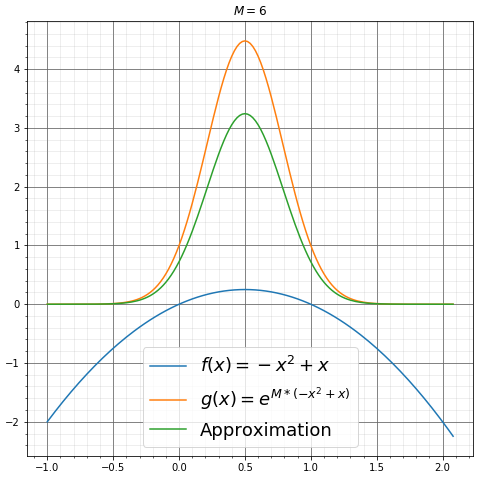
分别为\(M=1, 2, 3, 4, 5, 6\)时的函数图像。
3.2 斯图灵公式(Stirling Formula)
已知:\(\Gamma(z) = \int_0^\infty e^{-t} t^{z-1} dt\),且\(N! = \Gamma(N+1)\),下面尝试将阶乘\(N!\)表达为积分:
\[\begin{aligned} N! &= \int_0^\infty e^{-t} t^N dt \\ &= \int_0^\infty e^{-t + N \ln t} dt \end{aligned} \tag{8}\]令\(t = N \times s\),其中\(s>0\),则\(dt = Nds\),上式写为:
\[\begin{aligned} N! &= \int_0^\infty e^{-Ns + N \ln Ns} Nds \\ &= \int_0^\infty e^{-Ns + N \ln N + N \ln s} Nds \\ &= \int_0^\infty e^{-Ns + N \ln s} N^NN ds \\ &= N^{N+1}\int_0^\infty e^{N(-s + \ln s)} ds \end{aligned} \tag{9}\]其中,\(h(s) = -s + \ln s\)为极大值点在\(s_0 = 1\)取得的函数,满足Laplace’s方法的特殊情况,当\(N\)取一个非常大的值时:
\[\begin{aligned} N! &= N^{N+1}\int_0^\infty e^{N(-s + \ln s)} ds \\ &\approx N^{N+1} \sqrt{\frac{2\pi}{N \vert h''(s_0) \vert}} \times e^{Nh(s_0)} \\ &= N^{N+1} \sqrt{\frac{2\pi}{N}} e^{-N} \\ &= N^{N+1/2} \sqrt{2\pi} e^{-N} \end{aligned} \tag{10}\]对上式两边同时取对数:
\[\begin{aligned} \ln N! &\approx \ln [N^{N+1/2}] + \ln \sqrt{2\pi} + \ln e^{-N} \\ &\approx N \ln N - N \end{aligned} \tag{11}\]在式\((11)\)中,由于\(N\)取非常大的值,所以\(N^{1/2}\)和\(\ln \sqrt{2\pi}\)可以忽略。得到最终的式子即为斯图灵公式(Stirling Formula)。
尝试使用式\((10)\)进行阶乘的估算:
import numpy as np
def factorial(N):
ret = 1
for i in range(1, N+1):
ret *= i
return ret
def approx_factorial(N):
'''
N^{N+1/2} \sqrt{2\pi} e^{-N}
'''
return np.power(N, N+1/2) * np.sqrt(2*np.pi) * np.exp(-N)
for i in [1, 5, 10, 15]:
res = factorial(i)
app = approx_factorial(i)
print(f'N = {i:2}, result = {res:14}, approximation = {app:19}')
得到输出结果:
N = 1, result = 1, approximation = 0.9221370088957891
N = 5, result = 120, approximation = 118.01916795759007
N = 10, result = 3628800, approximation = 3598695.6187410355
N = 15, result = 1307674368000, approximation = 1300430722199.4658
可以看到,当\(N\)越大,Laplace’s方法估计的结果越准确