Understanding Support Vector Machines I
1. 前言
支持向量机(support vector machines, SVM)是一种二分类模型,基本做法是找到一个超平面把特征空间中的样本划分开来。李航老师的《统计学习方法》中把支持向量机分为三类:
- 线性可分支持向量机
- 线性支持向量机
- 非线性支持向量机
第一类指样本在特征空间中完全线性可分,这种情况非常理想,从该条件下入手推导公式容易理解;第二类指样本不是完全线性可分,可能存在噪声,所以需要对求解算法进行一点点改进;第三种指分类问题是非线性的,需要借助核技巧(kernel trick)。本文介绍前两种,后续博客中再介绍第三种。
学习支持向量机之前还有一个简单的概念需要理解:超平面(hyperplane),它是指在\(n\)维空间中,\(n-1\)维的子空间。例如线的超平面是点,面的超平面是线,三维空间的超平面是面。
2. 线性可分支持向量机
先从简单的条件出发,考虑样本线性可分,假设给定大小为\(N\)的数据集:
\[T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\}\]其中,\(x_i \in \mathbb{R}^n\),\(y_i \in \{+1, -1\}\),\(i=1, 2, \cdots, N\),\(x_i\)为第\(i\)个样本在特征空间中的特征向量。
2.1 硬间隔最大化
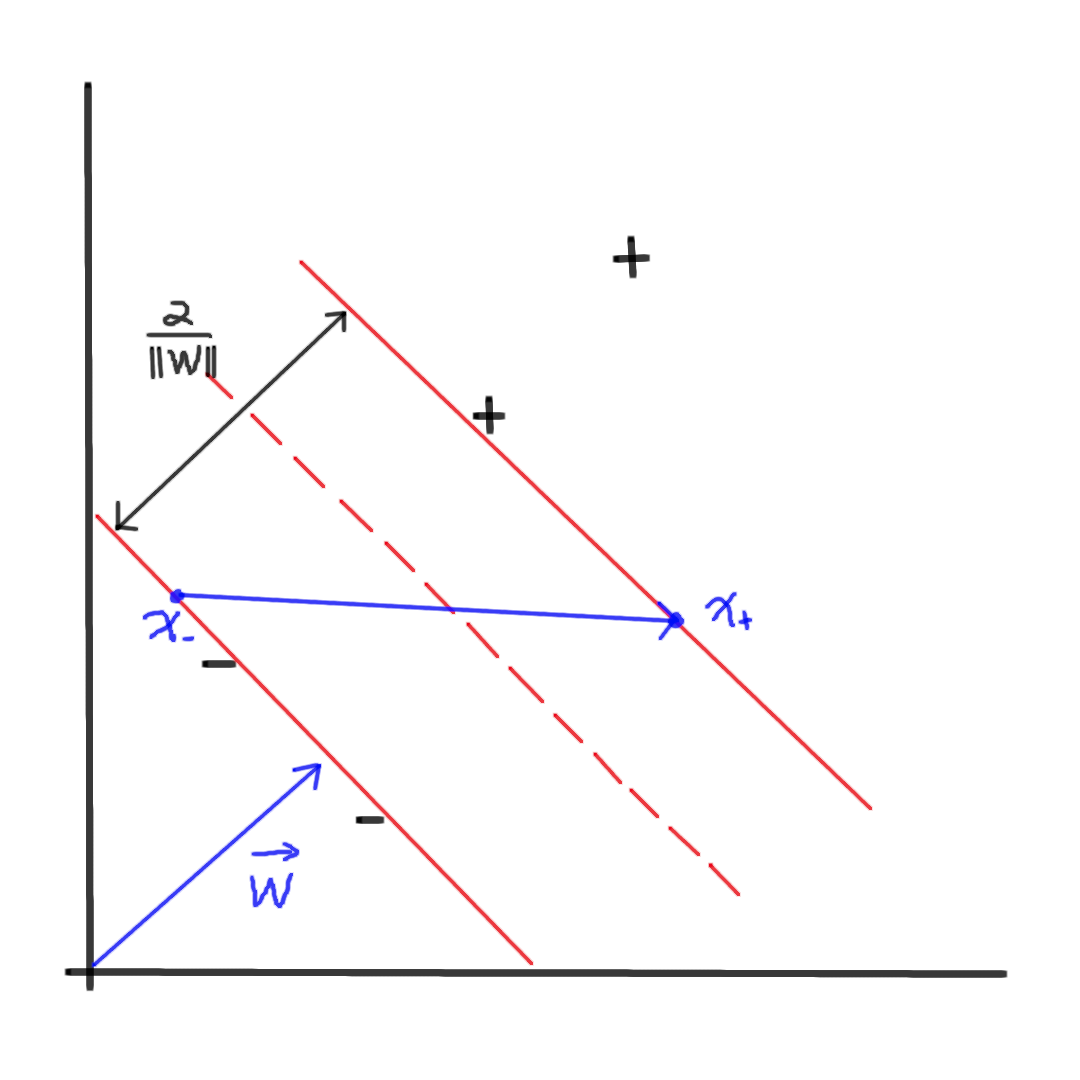
考虑如上二维情形,我们希望找到一个超平面(如红色虚线所示)使得正负样本尽可能被划分开,其中\(w\)是超平面的法向量,对于任意样本\(x\),它在\(w\)上的投影表示为:\(w \bullet x\),如果投影大于某个常数,即\(w \bullet x \geq b\),则为正样本,反之则为负样本。
那么基本决策如下:
\[\begin{aligned} w \bullet x + b &\geq 0, \ y = 1 \\ w \bullet x + b &< 0, \ y = -1 \end{aligned} \tag{2.1}\]对样本\(x_i\),其标签为\(y_i\),将式\(2.1\)简化得到:
\[(w \bullet x_i + b) * y_i \geq 0 \tag{2.2}\]我们可以将式\(2.2\)的条件设置得更加苛刻:
\[(w \bullet x_i + b) * y_i \geq 1 \tag{2.3}\]式\(2.3\)计算得到的结果即是样本点\(x_i\)到超平面的距离,表示为:
\[\gamma_i = (w \bullet x_i + b) * y_i \tag{2.4}\]此时将\(w\),\(b\)变为\(2w\),\(2b\),是不会影响优化过程的,所以一般限制\(\| w \| = 1\)。
现在的目的是找到一个超平面,使得正负样本与它的距离尽可能大(如图红色实线所示),假设红色实线上有负样本点\(x_{-}\)和正样本点\(x_{+}\),它们是距离超平面最近的点,那么这个超平面划分的宽度\(D\)为(\(w\)在向量\(\vec{x_{-}x_{+}}\)上的投影):
\[D = (x_{+} - x_{-}) * \frac{w}{\| w \|} \tag{2.5}\]观察式\(2.4\),不妨假设\(\gamma_i\)为1,得到:
\[\begin{aligned} w \bullet x_{+} &= 1 - b \\ - w \bullet x_{-} &= 1 + b \end{aligned} \tag{2.6}\]将式\(2.6\)代入式\(2.5\),得到:
\[D = \frac{2}{\| w \|} \tag{2.7}\]最大化\(D\)等价于最小化\(\frac{1}{2} \| w \|^2\)。
所以,最终的优化目标函数如下:
\[\begin{aligned} & \min_{w, b} \frac{1}{2} \| w \|^2 \\ & s.t. (w \bullet x_i + b) * y_i - 1 \geq 0, \ i = 1, 2, \cdots, N \end{aligned} \tag{2.8}\]2.2 求解对偶问题(拉格朗日函数)
为了求解式\(2.8\)的最优化问题,将它作为原始最优化问题,应用拉格朗日对偶性,通过求解对偶问题(dual problem)来得到原始问题(primal problem)的最优解,这么做的优点是:1. 对偶问题往往更容易求解;2. 自然引入核函数,进而推广到非线性分类问题。
构建拉格朗日函数(Lagrange function),对每一个不等式约束引入拉格朗日乘子(Lagrange multiplier)\(\alpha_i \geq 0\),\(i=1, 2, \cdots, N\),拉格朗日函数定义如下:
\[L(w, b, \alpha) = \frac{1}{2} \| w \|^2 - \sum_{i=1}^N \alpha_i y_i (w \bullet x_i + b) + \sum_{i=1}^{N} \alpha_i \tag{2.9}\]其中\(\alpha = (\alpha_1, \alpha_2, \cdots, \alpha_N)^T\)为拉格朗日乘子向量。
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
\[\max_{\alpha} \min_{w, b} L(w, b, \alpha)\]第一步求\(\min_{w, b} L(w, b, \alpha)\),令函数对\(w\)和\(b\)偏导为0:
\[\begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{N}\alpha_i y_i x_i = 0 \\ \frac{\partial L}{\partial b} &= -\sum_{i=1}^{N} \alpha_i y_i = 0 \end{aligned}\]得到:
\[\begin{aligned} & w = \sum_{i=1}^{N}\alpha_i y_i x_i \\ & \sum_{i=1}^{N} \alpha_i y_i = 0 \end{aligned} \tag{2.10}\]到这一步我们可以观察到\(w\)其实是由所有样本的特征向量构成的,其参与的比例由\(\alpha\)控制。
将式\(2.10\)代入式\(2.9\),得到:
\[\begin{aligned} \min_{w, b} L(w, b, \alpha) &= \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) - \sum_{i=1}^{N} \alpha_i y_i ((\sum_{j=1}^{N}\alpha_j y_j x_j) \bullet x_i + b) + \sum_{i=1}^{N}\alpha_i \\ &= -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) + \sum_{i=1}^{N}\alpha_i \end{aligned} \tag{2.11}\]第二步求\(\max_{\alpha} \min_{w, b} L(w, b, \alpha)\),即对偶问题:
\[\begin{aligned} \max_{\alpha} & -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) + \sum_{i=1}^{N}\alpha_i \\ s.t. & \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & \alpha_i \geq 0, \ i = 1, 2, \cdots, N \end{aligned} \tag{2.12}\]将最大化转变为最小化:
\[\begin{aligned} \min_{\alpha} & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) - \sum_{i=1}^{N}\alpha_i \\ s.t. & \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & \alpha_i \geq 0, \ i = 1, 2, \cdots, N \end{aligned} \tag{2.13}\]所以利用支持向量机求解线性可分问题转变为求解式\(2.13\),在计算得到最优解\(\alpha^* = (\alpha_1^*, \alpha_2^*, \cdots, \alpha_N^*)^T\)后,可以进一步得到\(w^*\):
\[w^* = \sum_{i=1}^{N} \alpha_i^* y_i x_i\]通过式\(2.4\)可以进一步得到\(b^*\):
\[b^* = y_j - w^* \bullet x_j = y_j - \sum_{i=1}^{N} \alpha^* y_i (x_i \bullet x_j)\]最后得到最优超平面:
\[w^* \bullet x + b^* = 0 \tag{2.14}\]2.3 支持向量
所谓支持向量,其实就是训练数据集中对应于\(\alpha_i^* > 0\)的样本\(x_i \in \mathbb{R}^n\),如果\(\alpha_i^* = 0\),那么根据式\(2.10\),对应的样本不会对\(w\)有任何贡献,所以不属于支持向量。
3. 线性支持向量机
通常情况下,训练数据中有一些特异点(outlier),将这些特异点除去后,剩下大部分样本点组成的集合是线性可分的,这意味着存在一些样本不满足式\(2.3\)。
3.1 软间隔最大化
为了解决这个问题,对每个样本点\((x_i, y_i)\)引入一个松弛变量\(\xi_i \geq 0\),使得约束条件变为:
\[(w \bullet x_i + b) * y_i \geq 1 - \xi_i \tag{3.1}\]同时,对每个松弛变量\(\xi_i\)施加惩罚,目标函数变为:
\[\frac{1}{2} \| w \|^2 + C \sum_{i=1}^{N} \xi_i\]其中,\(C>0\)为常数,作为惩罚参数。
所以,对应于式\(2.8\),此时的最优化原始问题为:
\[\begin{aligned} \min_{w, b, \xi} & \frac{1}{2} \| w \|^2 + C \sum_{i=1}^{N} \xi_i \\ s.t. & (w \bullet x_i + b) * y_i - 1 + \xi_i \geq 0, \ i = 1, 2, \cdots, N \\ & \xi_i \geq 0, \ i = 1, 2, \cdots, N \end{aligned} \tag{3.2}\]构建拉格朗日函数为:
\[L(w, b, \xi, \alpha, \mu) = \frac{1}{2} \| w \|^2 + C \sum_{i=1}^{N} \xi_i - \sum_{i=1}^{N} \alpha_i (y_i(w \bullet x_i + b) - 1 + \xi_i) - \sum_{i=1}^{N} \mu_i \xi_i \tag{3.3}\]其中,\(\alpha_i \geq 0\),\(\mu_i \geq 0\)。
首先求\(L(w, b, \xi, \alpha, \mu)\)对\(w\),\(b\),\(\xi\)的极小,求偏导并令其为0:
\[\begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{N}\alpha_i y_i x_i = 0 \\ \frac{\partial L}{\partial b} &= - \sum_{i=1}^{N} \alpha_i y_i = 0 \\ \frac{\partial L}{\partial \xi} &= C - \alpha_i - \mu_i = 0 \end{aligned} \tag{3.4}\]得到:
\[\begin{aligned} w &= \sum_{i=1}^{N}\alpha_i y_i x_i \\ & \sum_{i=1}^{N} \alpha_i y_i = 0 \\ C & - \alpha_i - \mu_i = 0 \end{aligned} \tag{3.5}\]将式\(3.5\)代入式\(3.3\),得到:
\[\min_{w, b, \xi} L(w, b, \xi, \alpha, \mu) = -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) + \sum_{i=1}^{N} \alpha_i \tag{3.6}\]再对\(\min_{w, b, \xi} L(w, b, \xi, \alpha, \mu)\)求\(\alpha\)的极大,即得到对偶问题:
\[\begin{aligned} \max_\alpha & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) + \sum_{i=1}^{N} \alpha_i \\ s.t. & \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & C - \alpha_i - \mu_i = 0 \\ & \alpha_i \geq 0 \\ & \mu_i \geq 0, \ i=1, 2, \cdots, N \end{aligned} \tag{3.7}\]化简式\(3.7\),得到:
\[\begin{aligned} \min_\alpha & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (x_i \bullet x_j) - \sum_{i=1}^{N} \alpha_i \\ s.t. & \sum_{i=1}^{N} \alpha_i y_i = 0 \\ & 0 \leq \alpha_i \leq C, \ i=1, 2, \cdots, N \end{aligned} \tag{3.8}\]以上就是带有松弛变量的支持向量机的公式推导,本质上就是在最优化问题中多了一个限制,构建拉格朗日函数过程中多加一项,并且在推导过程中不断化简。
参考
《统计学习方法》, 李航
Hyperplane
MIT 6.034 Artificial Intelligence, Fall 2010